如图1,矩形
(1) 如图2, 当
(2) 如图3, 连接
(3) 当
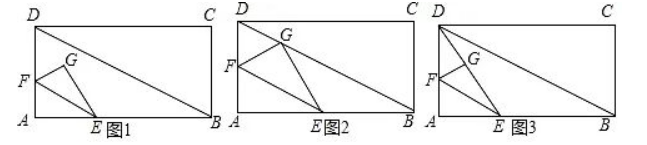
(1) 如图2, 当
(2) 如图3, 连接
(3) 当
