图 1 是一种推磨工具模型，图 2 是它的示意图，已知 $A B \perp P Q, A P=A Q=3 d m, A B=12 d m$, 点 $A$ 在中轴 线 $l$ 上运动, 点 $B$ 在以 $O$ 为圆心, $O B$ 长为半径的圆上运动, 且 $O B=4 d m$.

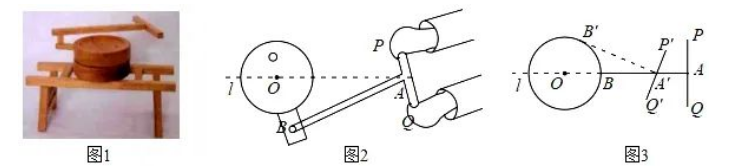
(1) 如图3, 当点 $B$ 按送时针方向运动到 $B^{\prime}$ 时, $A^{\prime} B^{\prime}$ 与 $\odot O$ 相切, 则 $A A'$
(2) 在点 $B$ 的运动过程中, 点 $P$ 与点 $O$ 之间的最短距离为