如图,已知
(1) 求证:
(2) 若半径为 2 , 求图中线段
(3) 在 (2) 的条件
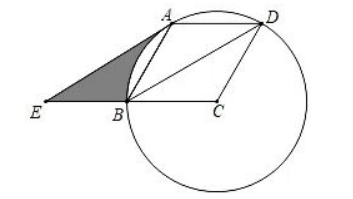
(1) 求证:
(2) 若半径为 2 , 求图中线段
(3) 在 (2) 的条件
