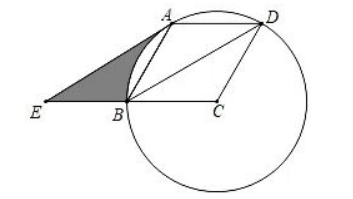
如图，已知 $\odot C$ 过菱形 $A B C D$ 的三个顶点 $B, A, D$, 连结 $B D$, 过点 $A$ 作 $A E \| B D$ 交射线 $C B$ 于点 $E$.
(1) 求证: $A E$ 是 $\odot C$ 的切线.
(2) 若半径为 2 , 求图中线段 $A E$ 、线段 $B E$ 和 $\widehat{\mathrm{AB}}$ 围成的部分的面积.
(3) 在 (2) 的条件 $F$, 在 $\odot C$ 上取点 $F$, 连结 $A F$, 使 $\angle D A F=15^{\circ}$, 求点 $F$ 到直线 $A D$ 的距离.