我们知道求函数图象的交点坐标，可以联立两个函数解析式组成方程组，方程组的解就是交点的坐 标. 如：求直线 $y=2 x+3$ 与 $y=-x+6$ 的交点坐标，我们可以联立两个解析式得到方程组 $\left\{\begin{array}{l}y=2 x+3 \\ y=-x+6\end{array}\right.$, 解得 $\left\{\begin{array}{l}\mathrm{x}=1 \\ \mathrm{y}=5\end{array}\right.$, 所以直线 $y=2 x+3$ 与 $y=-x+6$ 的交点坐标为 $(1 ， 5)$. 请利用上述知识解决下列问题:
(1) 已知直线 $y=k x-2$ 和扡物线 $y=x^2-2 x+3$ ，
① 当 $k=4$ 时, 求直线与抛物线的交点坐标;
②当 $k$ 为何值时, 直线与拋物线只有一个交点?

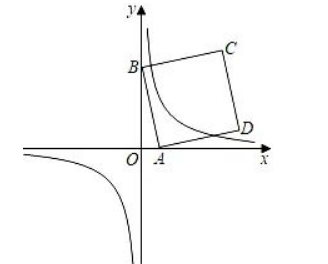
(2) 已知点 $A(a, 0)$ 是 $x$ 轴上的动点, $B(0,4 \sqrt{2})$, 以 $A B$ 为边在 $A B$ 右侧做正方形 $A B C D$, 当正方形 $2 \sqrt{2}$
$A B C D$ 的边与反比例函数 $y=\overline{\mathrm{x}}$ 的图象有 4 个交点时, 试求 $a$ 的取值范围.