单选题 (共 4 题 ),每题只有一个选项正确
已知 $P$ 是边长为 2 的菱形 $A B C D$ 内一点, 若 $\angle B A D=120^{\circ}$, 则 $\overrightarrow{A P} \cdot \overrightarrow{A B}$ 的取值范围是
$\text{A.}$ $(-2,4)$
$\text{B.}$ $(-2,2)$
$\text{C.}$ $(2,4)$
$\text{D.}$ $(-4,2)$
在数学中, 有一个被称为自然常数 (又叫欧拉数) 的常数 $e \approx 2.71828$. 小 明在设置银行卡的数字密码时, 打算将自然常数的前 6 位数字 $2,7,1$, $8,2,8$ 进行某种排列得到密码. 如果排列时要求 2 不排第一个, 两个 8 相邻,那么小明可以设置的不同的密码个数为
$\text{A.}$ 30
$\text{B.}$ 32
$\text{C.}$ 36
$\text{D.}$ 48
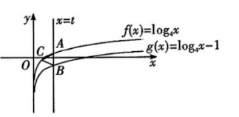
如图, 直线 $x=t$ 与函数 $f(x)=\log _4 x$ 和 $g(x)=\log _4 x-1$ 的图象分别交于点 $A, B$, 若函数 $y=f(x)$ 的图象上存在一 点 $C$, 使得 $\triangle A B C$ 为等边三角形, 则 $t$ 的值为
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{3 \sqrt{3}}{4}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\frac{3 \sqrt{3}}{2}$
在平面直角坐标系中, $A(2,0), B(0,2)$. 以下各曲线: (1) $\frac{x^2}{3}+\frac{y^2}{2}=1$; (2) $(x+2)^2+y^2=2$; (3) $y^2=2 x$; (4) $x^2-y^2=1$ 中, 存在两个不同的点 $M$, $N$,使得 $|M A|=|M B|$ 且 $|N A|=|N B|$ 的曲线是
$\text{A.}$ (1)(2)
$\text{B.}$ (3)(4)
$\text{C.}$ (2)(4)
$\text{D.}$ (1)(3)
多选题 (共 2 题 ),每题有多个选项正确
已知函数 $f(x)=|\sin x|+\cos x$, 则下述结论正确是
$\text{A.}$ $f(x)$ 是偶函数
$\text{B.}$ $f(x)$ 的周期是 $\pi$
$\text{C.}$ 函数 $f(x)$ 的图象关于直线 $x=\pi$ 对称
$\text{D.}$ $f(x)$ 的值域为 $[-1, \sqrt{2}]$
已知函数 $f(x)=\ln |x|-x+\frac{1}{x}$, 则下列说法正确的是
$\text{A.}$ $f(x)$ 在 $(0,+\infty)$ 上单调递减
$\text{B.}$ $f(x)$ 恰有 2 个零点
$\text{C.}$ 若 $x_1 \neq x_2, f\left(x_1\right)-f\left(x_2\right)=0$, 则 $x_1 x_2 \leqslant-1$
$\text{D.}$ 若 $x_1>x_2>0, f\left(x_1\right)+f\left(x_2\right)=0$, 则 $x_1 x_2=1$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
等差数列 $\left\{a_n\right\}$ 满足 $a_2=6, a_4+a_5=27$. 等比数列 $\left\{b_n\right\}$ 为递增数列, 且 $b_1, b_2, b_3 \in\{2,3,4,5,8\}$.
(1)求数列 $\left\{a_n\right\}$ 和 $\left\{b_n\right\}$ 的通项公式;
(2) 删去数列 $\left\{b_n\right\}$ 中的 $b_{a_4}$ 项 (其中 $k=1,2,3, \cdots$ ), 保持剩余项的顺序不 变, 组成新数列 $\left\{c_n\right\}$, 求数列 $\left\{c_n\right\}$ 的前 10 项和 $T_{10}$.
在四边形 $A B C D$ 中, $A B / / C D, A D=B D=C D=1$.
(1) 若 $A B=\frac{3}{2}$, 求 $B C$;
(2)若 $A B=2 B C$, 求 $\cos \angle B D C$.
受新冠病毒感染影响, 部分感染的学生身体和体能发生了变化. 为了了 解学生的运动情况, 某中学对高中三个年级的学生运动情况进行了分 层抽样调查. 调查的样本中高一年级有 $70 \%$ 的学生每周运动总时间超 过 5 小时, 高二年级有 $65 \%$ 的学生每周运动总时间超过 5 小时, 高三 年级有 $56 \%$ 的学生每周运动总时间超过 5 小时, 且三个年级的学生人 数之比为 $9: 6: 5$, 用样本的频率估计总体的概率.
(1) 从该校三个年级中随机抽取 1 名学生, 估计该学生每周运动总时间 超过 5 小时的概率;
(2)假设该校每名学生每周运动总时间为随机变量 $X$ (单位: 小时), 且 $X \sim N\left(5.5, \sigma^2\right)$. 现从这三个年级中随机抽取 3 名学生, 设这 3 名学 生中每周运动总时间为 5 至 6 小时的人数为 $Y$, 求随机变量 $Y$ 的 期望.
已知函数 $f(x)=\mathrm{e}^x+\cos x-m x, x \in(0,+\infty)$.
(1) 若函数 $f(x)$ 在 $(0, \pi)$ 上单调递减, 求实数 $m$ 的取值范围;
(2) 若 $\mathrm{e}^{\frac{\pi}{2}}-1 < m < \mathrm{e}^\pi$, 求证: 函数 $f(x)$ 有两个零点. (参考数据: $\mathrm{e}^{\frac{\pi}{2}} \approx$ 4. $81, \mathrm{e}^\pi \approx 23.14$ )
在平面直角坐标系中, $M(-3,0), N(3,0), P$ 为曲线 $E$ 上一点, 直线 $M P, N P$ 的斜率之积为 $-\frac{5}{9}$.
(1)求曲线 $E$ 的标准方程;
(2) 过点 $F(2,0)$ 作直线 $l$ 交曲线 $E$ 于 $A, B$ 两点, 且点 $A$ 位于 $x$ 轴的上 方, 记直线 $M B, N A$ 的斜率分别为 $k_1, k_2$.
(1) 证明: $\frac{k_1}{k_2}$ 为定值;
(ii) 过点 $B$ 作 $B C$ 垂直 $x$ 轴交曲线 $E$ 于不同于点 $A$ 的点 $C$, 直线 $A C$ 与 $x$ 轴交于点 $D$, 求 $\triangle A D F$ 面积的最大值.