单选题 (共 8 题 ),每题只有一个选项正确
碘125衰变时产生 射线,医学上利用此特性可治疗某些疾病。碘125的半衰期为60天,若将一定质量的碘125植入患者病灶组织,经过180天剩余碘125的质量为刚植入时的
$\text{A.}$ $\frac{1}{16}$
$\text{B.}$ $\frac{1}{8}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{2}$
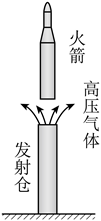
我国多次成功使用“冷发射”技术发射长征十一号系列运载火箭。如图所示,发射仓内的高压气体先将火箭竖直向上推出,火箭速度接近零时再点火飞向太空。从火箭开始运动到点火的过程中
$\text{A.}$ 火箭的加速度为零时,动能最大
$\text{B.}$ 高压气体释放的能量全部转化为火箭的动能
$\text{C.}$ 高压气体对火箭推力的冲量等于火箭动量的增加量
$\text{D.}$ 高压气体的推力和空气阻力对火箭做功之和等于火箭动能的增加量
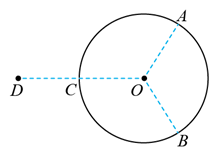
半径为 $R$ 的绝缘细圆环固定在图示位置, 圆心位于 $O$ 点, 环上均匀份布着电量为 $Q$ 的正电荷。点 $A 、 B 、$ $C$ 将圆环三等分, 取走 $A 、 B$ 处两段弧长均为 $\Delta L$ 的小圆弧上的电荷。将一点电荷 $q$ 置于 $O C$ 延长线上距 $O$ 点为 $2 R$ 的 $D$ 点, $O$ 点的电场强度刚好为零。圆环上剩余电荷分布不变, $q$ 为
$\text{A.}$ 正电荷, $q=\frac{Q \Delta L}{\pi R}$
$\text{B.}$ 正电荷, $q=\frac{\sqrt{3} Q \Delta L}{\pi R}$
$\text{C.}$ 负电荷, $q=\frac{2 Q \Delta L}{\pi R}$
$\text{D.}$ 负电荷, $q=\frac{2 \sqrt{3} Q \Delta L}{\pi R}$
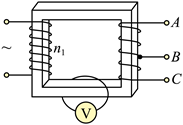
如图所示的变压器, 输入电压为 $220 \mathrm{~V}$, 可输出 $12 \mathrm{~V} 、 18 \mathrm{~V} 、 30 \mathrm{~V}$ 电压, 匝数为 $n_1$ 的原线圈中电随时间 变化为 $\mu=U_{\mathrm{m}} \cos (100 \pi t)$. 单匝线圈绕过铁芯连接交流电压表, 电压表的示数为 $0.1 \mathrm{~V}$ 。将阻值为 $12 \Omega$ 的电阻 $R$ 接在 $B C$ 两端时, 功率为 $12 \mathrm{~W}$ 。下列说法正确的是
$\text{A.}$ $n_1$ 为 1100 匝, $U_{\mathrm{m}}$ 为 $220 \mathrm{~V}$
$\text{B.}$ $B C$ 间线圈匝数为 120 匝, 流过 $R$ 的电流为 $1.4 \mathrm{~A}$
$\text{C.}$ 若将 $R$ 接在 $A B$ 两端, $R$ 两端的电压为 $18 \mathrm{~V}$, 频率为 $100 \mathrm{~Hz}$
$\text{D.}$ 若将 $R$ 接在 $A C$ 两端, 流过 $R$ 的电流为 $2.5 \mathrm{~A}$, 周期为 $0.02 \mathrm{~s}$
如图所示,内壁光滑的绝热气缸内用绝热活塞封闭一定质量的理想气体,初始时气缸开口向上放置,活塞处于静止状态,将气缸缓慢转动90度过程中,缸内气体
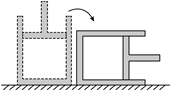
$\text{A.}$ 内能增加,外界对气体做正功
$\text{B.}$ 内能减小,所有分子热运动速率都减小
$\text{C.}$ 温度降低,速率大的分子数占总分子数比例减少
$\text{D.}$ 温度升高,速率大的分子数占总分子数比例增加
“羲和号” 是我国首颗太阳探测科学技术试验卫星。如图所示, 该卫星围绕地球的运动视为匀速圆周运 动, 轨道平面与赤道平面接近垂直。卫星每天在相同时刻, 沿相同方向经过地球表面 $A$ 点正上方, 恰好绕 地球运行 $n$ 圈。已知地球半径为地轴 $R$, 自转周期为 $T$, 地球表面重力加速度为 $g$, 则 “羲和号” 卫星轨道 距地面高度为
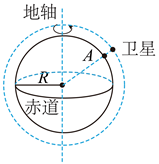
$\text{A.}$ $\left(\frac{g R^2 T^2}{2 n^2 \pi^2}\right)^{\frac{1}{3}}-R$
$\text{B.}$ $\left(\frac{g R^2 T^2}{2 n^2 \pi^2}\right)^{\frac{1}{3}}$
$\text{C.}$ $\left(\frac{g R^2 T^2}{4 n^2 \pi^2}\right)^{\frac{1}{3}}-R$
$\text{D.}$ $\left(\frac{g R^2 T^2}{4 n^2 \pi^2}\right)^{\frac{1}{3}}$
柱状光学器件横截面如图所示, $O P$ 右侧是以 $O$ 为圆心、半径为 $R$ 的 $\frac{1}{4}$ 圆, 左则是直角梯形, $A P$ 长为 $R, A C$ 与 $C O$ 夹角 $45^{\circ}, A C$ 中点为 $B \circ a 、 b$ 两种频率的细激光束, 垂直 $A B$ 面入射, 器件介质对 $a, b$ 光的折射率分别为 $1.42 、 1.40$ 。保持光的入射方向不变, 入射点从 $A$ 向 $B$ 移动过程中, 能在 $P M$ 面全反射 后, 从 $O M$ 面射出的光是 (不考虑三次反射以后的光)
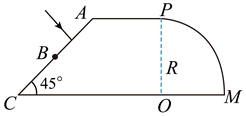
$\text{A.}$ 仅有 $a$ 光
$\text{B.}$ 仅有 $b$ 光
$\text{C.}$ $a 、 b$ 光都可以
$\text{D.}$ $a 、 b$ 光都不可以
无人配送小车某次性能测试路径如图所示, 半径为 $3 \mathrm{~m}$ 的半圆弧 $B C$ 与长 $8 \mathrm{~m}$ 的直线路径 $A B$ 相切于 $B$ 点, 与半径为 $4 \mathrm{~m}$ 的半圆弧 $C D$ 相切于 $C$ 点。小车以最大速度从 $A$ 点驶入路径, 到适当位置调整速率运动 到 $B$ 点, 然后保持速率不变依次经过 $B C$ 和 $C D$ 。为保证安全, 小车速率最大为 $4 \mathrm{~m} / \mathrm{s}$ 。在 $A B C$ 段的加速 度最大为 $2 \mathrm{~m} / \mathrm{s}^2, C D$ 段的加速度最大为 $1 \mathrm{~m} / \mathrm{s}^2$ 。小车视为质点, 小车从 $A$ 到 $D$ 所需最短时间 $t$ 及在 $A B$ 段做匀速直线运动的最长距离 $l$ 为
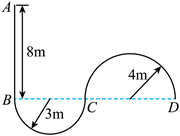
$\text{A.}$ $t=\left(2+\frac{7 \pi}{4}\right) \mathrm{s}, l=8 \mathrm{~m}$
$\text{B.}$ $t=\left(\frac{9}{4}+\frac{7 \pi}{2}\right) \mathrm{s}, l=5 \mathrm{~m}$.
$\text{C.}$ $t=\left(2+\frac{5}{12} \sqrt{6}+\frac{7 \sqrt{6} \pi}{6}\right) \mathrm{s}, l=5.5 \mathrm{~m}$.
$\text{D.}$ $t=\left[2+\frac{5}{12} \sqrt{6}+\frac{(\sqrt{6}+4) \pi}{2}\right] \mathrm{s}, l=5.5 \mathrm{~m}$
多选题 (共 4 题 ),每题有多个选项正确
某同学采用图甲所示的实验装置研究光的干涉与衍射现象, 狭缝 $S_1, S_2$ 的宽度可调, 狭缝到屏的距离 为 $L$ 。同一单色光垂直照射狭缝, 实验中分别在屏上得到了图乙, 图丙所示图样。下列描述正确的是
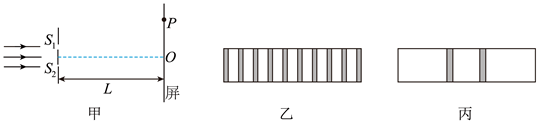
$\text{A.}$ 图乙是光的双缝干涉图样,当光通过狭缝时,也发生了衍射
$\text{B.}$ 遮住一条狭缝,另一狭缝宽度增大,其他条件不变,图丙中亮条纹宽度增大
$\text{C.}$ 照射两条狭缝时,增加L,其他条件不变,图乙中相邻暗条纹的中心间距增大
$\text{D.}$ 照射两条狭缝时,若光从狭缝$S_1$ 、$S_2$ 到屏上P点的路程差为半波长的奇数倍,P点处一定是暗条纹
如图所示, 某同学将离地 $1.25 \mathrm{~m}$ 的网球以 $13 \mathrm{~m} / \mathrm{s}$ 的速度斜向上击出, 击球点到坚直墙壁的距离 $4.8 \mathrm{~m}$ 。当 网球坚直分速度为零时, 击中墙壁上离地高度为 $8.45 \mathrm{~m}$ 的 $P$ 点。网球与墙壁碰撞后, 垂直墙面速度分量大 小变为碰前的 0.75 倍。平行墙面的速度分量不变。重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 网球碰墙后的速度大小 $v$ 和 着地点到墙壁的距离 $d$ 分别为

$\text{A.}$ $v=5 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ $v=3 \sqrt{2} \mathrm{~m} / \mathrm{s}$
$\text{C.}$ $d=3.6 \mathrm{~m}$
$\text{D.}$ $d=3.9 \mathrm{~m}$
如图所示, $x O y$ 平面的第一、三象限内以坐标原点 $O$ 为圆心、半径为 $\sqrt{2} L$ 的扇形区域充满方向垂直 纸面向外的匀强磁场。边长为 $L$ 的正方形金属框绕其始终在 $O$ 点的顶点、在 $x O y$ 平面内以角速度 $\omega$ 顺时 针匀速转动, $t=0$ 时刻, 金属框开始进入第一象限。不考虑自感影响, 关于金属框中感应电动势 $E$ 随时 间 $t$ 变化规律的描述正确的是
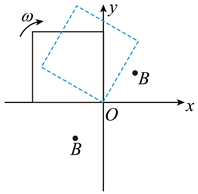
$\text{A.}$ 在 $t=0$ 到 $t=\frac{\pi}{2 \omega}$ 的过程中, $E$ 一直增大
$\text{B.}$ 在 $t=0$ 到 $t=\frac{\pi}{2 \omega}$ 的过程中, $E$ 先增大后减小
$\text{C.}$ 在 $t=0$ 到 $t=\frac{\pi}{4 \omega}$ 的过程中, $E$ 的变化率一直增大
$\text{D.}$ 在 $t=0$ 到 $t=\frac{\pi}{4 \omega}$ 的过程中, $E$ 的变化率一直减小
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在天宫课堂中、我国航天员演示了利用牛顿第二定律测量物体质量的实验。受此启发。某同学利用气垫导轨、力传感器、无线加速度传感器、轻弹簧和待测物体等器材设计了测量物体质量的实验,如图甲所示。主要步骤如下:
①将力传感器固定在气垫导轨左端支架上,加速度传感器固定在滑块上;
②接通气源。放上滑块。调平气垫导轨;
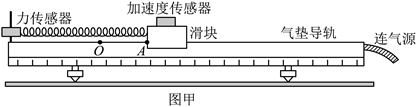
③将弹簧左端连接力传感器,右端连接滑块。弹簧处于原长时滑块左端位于O点。A点到O点的距离为5.00cm,拉动滑块使其左端处于A点,由静止释放并开始计时;
④计算机采集获取数据,得到滑块所受弹力F、加速度a随时间t变化的图像,部分图像如图乙所示。
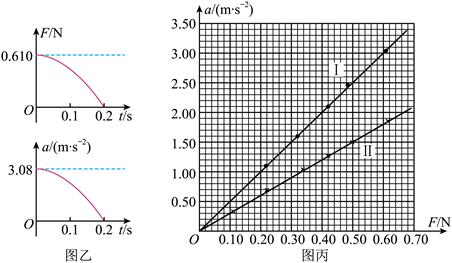
回答以下问题(结果均保留两位有效数字):
(1)弹簧的劲度系数为 ________ N/m。
(2)该同学从图乙中提取某些时刻F与a的数据,画出a—F图像如图丙中I所示,由此可得滑块与加速度传感器的总质量为 ________ kg。
(3)该同学在滑块上增加待测物体,重复上述实验步骤,在图丙中画出新的a—F图像Ⅱ,则待测物体的质量为 ________。
某同学利用实验室现有器材, 设计了一个测量电阻阻值的实验。实验器材:
干电池 $E$ (电动势 $1.5 \mathrm{~V}$, 内阻末知);
电流表 $A_1$ (量程 $10 \mathrm{~mA}$, 内阻为 $90 \Omega$ );
电流表 $\mathrm{A}_2$ (量程 $30 \mathrm{~mA}$, 内阻为 $30 \Omega$ );
定值电阻 $R_0$ (阻值为 $150 \Omega$ );
滑动变阻器 $R$ (最大阻值为 $100 \Omega$ );
待测电阻 $R_x$;
开关 $S$, 导线若干。
测量电路如图所示。
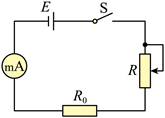
(1) 断开开关, 连接电路, 将滑动变阻器 $R$ 的滑片调到阻值最大一端。将定值电阻 $R_0$ 接入电路; 闭合开 关,调节滑片位置。使电流表指针指在满刻度的 $\frac{1}{2}$ 处。该同学选用的电流表为 ________ (填 “ $\mathrm{A}_1$ ”或“ $\mathrm{A}_2$ ” ); 若不考虑电池内阻。此时滑动变阻器接入电路的电阻值应为 ________ $\Omega$ 。
(2) 断开开关, 保持滑片的位置不变。用 $R_x$ 替换 $R_0$, 闭合开关后, 电流表指针指在满刻度的 $\frac{3}{5}$ 处, 则 $R_x$ 的测量值为 ________ $\Omega$ 。
(3) 本实验中末考虑电池内阻, 对 $R_x$ 的测量值 ________ (填 “有” 或 “无”)影响
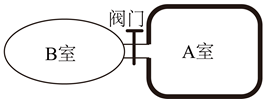
某些鱼类通过调节体内鱼鳔的体积实现浮沉。如图所示, 鱼鳔结构可简化为通过阀门相连的 $\mathrm{A} 、 \mathrm{~B}$ 两个密 闭气室, $\mathrm{A}$ 室壁厚、可认为体积恒定, $\mathrm{B}$ 室壁簿, 体积可变; 两室内气体视为理想气体, 可通过阀门进行 交换。质量为 $M$ 的鱼静止在水面下 $H$ 处。B 室内气体体积为 $V$, 质量为 $m$; 设 B 室内气体压强与鱼体外压 强相等、鱼体积的变化与 B 室气体体积的变化相等, 鱼的质量不变, 鱼鳔内气体温度不变。水的密度为 $\rho$, 重力加速度为 $g$ 。大气压强为 $p_0$, 求:
(1)鱼通过增加 $\mathrm{B}$ 室体积获得大小为 $a$ 的加速度、需从 $\mathrm{A}$ 室充入 $\mathrm{B}$ 室的气体质量 $\Delta m$;
(2)鱼静止于水面下 $H_1$ 处时, B 室内气体质量 $m_1$ 。
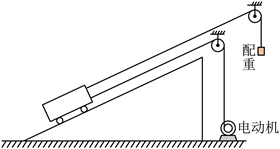
某粮库使用额定电压 $U=380 \mathrm{~V}$, 内阻 $R=0.25 \Omega$ 的电动机运粮。如图所示, 配重和电动机连接小车的缆 绳均平行于斜坡, 装满粮食的小车以速度 $v=2 \mathrm{~m} / \mathrm{s}$ 沿斜坡匀速上行, 此时电流 $I=40 \mathrm{~A}$ 。关闭电动机后, 小车又沿斜坡上行路程 L 到达卸粮点时, 速度恰好为零。卸粮后, 给小车一个向下的初速度, 小车沿斜坡 刚好匀速下行。已知小车质量 $m_1=100 \mathrm{~kg}$, 车上粮食质量 $m_2=1200 \mathrm{~kg}$, 配重质量 $m_0=40 \mathrm{~kg}$, 取重力 加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$, 小车运动时受到的摩擦阻力与车及车上粮食总重力成正比, 比例系数为 $k$, 配重始终 末接触地面, 不计电动机自身机械摩擦损耗及缆绳质量。求:
(1) 比例系数 $k$ 值;
(2) 上行路程 $L$ 值。
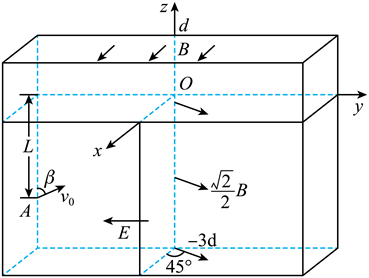
中国 “人造太阳” 在核聚变实验方而取得新突破, 该装置中用电磁场约束和加速高能离子, 其部分电磁场 简化模型如图所示, 在三维坐标系 $O x y z$ 中, $0 < z, d$ 空间内充满匀强磁场 I, 磁感应强度大小为 $B$, 方向 沿 $x$ 轴正方向; $-3 d, z < 0, y . .0$ 的空间内充满匀强磁场 II, 磁感应强度大小为 $\frac{\sqrt{2}}{2} B$, 方向平行于 $x O y$ 平面, 与 $x$ 轴正方向夹角为 $45^{\circ} ; z < 0, y \leq 0$ 的空间内充满沿 $\mathrm{y}$ 轴负方向的匀强电场。质量为 $m$ 、 带电量为 $+q$ 的离子甲, 从 $y O z$ 平面第三象限内距 $y$ 轴为 $L$ 的点 $\mathrm{A}$ 以一定速度出射, 速度方向与 $z$ 轴正方 向夹角为 $\beta$, 在在 $y O z$ 平面内运动一段时间后, 经坐标原点 $O$ 沿 $z$ 轴正方向进入磁场 $\mathrm{I}$ 。不计离子重力。
(1) 当离子甲从 $\mathrm{A}$ 点出射速度为 $v_0$ 时, 求电场强度的大小 $E$;
(2)若使离子甲进入磁场后始终在磁场中运动, 求进入磁场时的最大速度 $v_{\mathrm{m}}$;
(3) 离子甲以 $\frac{q B d}{2 m}$ 的速度从 $O$ 点沿 $z$ 轴正方向第一次穿过 $x O y$ 面进入磁场 $\mathrm{I}$, 求第四次穿过 $x O y$ 平面的 位置坐标 (用 $d$ 表示);
(4) 当离子甲以 $\frac{q B d}{2 m}$ 的速度从 $O$ 点进入磁场 $\mathrm{I}$ 时, 质量为 $4 m$ 、带电量为 $+q$ 的离子乙, 也从 $O$ 点沿 $z$ 轴 正方向以相同的动能同时进入磁场 $\mathrm{I}$, 求两离子进入磁场后, 到达它们运动轨迹第一个交点的时间差 $\Delta t$ (忽略离子间相互作用)。
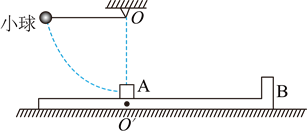
如图所示, “L” 型平板 B 静置在地面上, 小物块 A 处于平板 B 上的 $O^{\prime}$ 点, $O^{\prime}$ 点左侧粗粘, 右侧光滑。 用不可伸长的轻绳将质量为 $M$ 的小球悬挂在 $O^{\prime}$ 点正上方的 $O$ 点, 轻绳处于水平拉直状态。将小球由静止 释放, 下摆至最低点与小物块 $\mathrm{A}$ 发生碰撞, 碰后小球速度方向与碰前方向相同, 开始做简谐运动(要求摆 角小于 $\left.5^{\circ}\right), \mathrm{A}$ 以速度 $v_0$ 沿平板滑动直至与 $\mathrm{B}$ 右侧挡板发生弹性碰撞。一段时间后, $\mathrm{A}$ 返回到 $O$ 点的正下 方时, 相对于地面的速度减为零, 此时小球恰好第一次上升到最高点。已知 $\mathrm{A}$ 的质量 $m_{\mathrm{A}}=0.1 \mathrm{~kg}, \mathrm{~B}$ 的 质量 $m_{\mathrm{B}}=0.3 \mathrm{~kg}, \mathrm{~A}$ 与 $\mathrm{B}$ 的动摩擦因数 $\mu_1=0.4, \mathrm{~B}$ 与地面间的动摩擦因数 $\mu_2=0.225, v_0=4 \mathrm{~m} / \mathrm{s}$, 取 重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。整个过程中 $\mathrm{A}$ 始终在 $\mathrm{B}$ 上, 所有碰撞时间忽略不计, 不计空气阻力, 求:
(1) $\mathrm{A}$ 与 $\mathrm{B}$ 的挡板碰撞后, 二者的速度大小 $v_{\mathrm{A}}$ 与 $v_{\mathrm{B}}$;
(2) B 光滑部分的长度 $d$;
(3) 运动过程中 $\mathrm{A}$ 对 $\mathrm{B}$ 的摩擦力所做的功 $W_{\mathrm{f}}$;
(4) 实现上述运动过程, $\frac{M}{m_{\mathrm{A}}}$ 的取值范围 (结果用 $\cos 5^{\circ}$ 表示)。