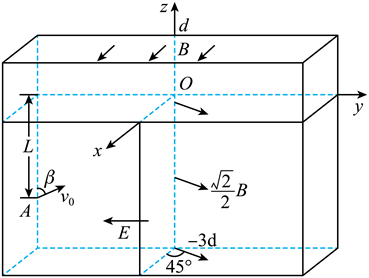
中国 “人造太阳” 在核聚变实验方而取得新突破, 该装置中用电磁场约束和加速高能离子, 其部分电磁场 简化模型如图所示, 在三维坐标系 $O x y z$ 中, $0 < z, d$ 空间内充满匀强磁场 I, 磁感应强度大小为 $B$, 方向 沿 $x$ 轴正方向; $-3 d, z < 0, y . .0$ 的空间内充满匀强磁场 II, 磁感应强度大小为 $\frac{\sqrt{2}}{2} B$, 方向平行于 $x O y$ 平面, 与 $x$ 轴正方向夹角为 $45^{\circ} ; z < 0, y \leq 0$ 的空间内充满沿 $\mathrm{y}$ 轴负方向的匀强电场。质量为 $m$ 、 带电量为 $+q$ 的离子甲, 从 $y O z$ 平面第三象限内距 $y$ 轴为 $L$ 的点 $\mathrm{A}$ 以一定速度出射, 速度方向与 $z$ 轴正方 向夹角为 $\beta$, 在在 $y O z$ 平面内运动一段时间后, 经坐标原点 $O$ 沿 $z$ 轴正方向进入磁场 $\mathrm{I}$ 。不计离子重力。
(1) 当离子甲从 $\mathrm{A}$ 点出射速度为 $v_0$ 时, 求电场强度的大小 $E$;
（2）若使离子甲进入磁场后始终在磁场中运动, 求进入磁场时的最大速度 $v_{\mathrm{m}}$;
(3) 离子甲以 $\frac{q B d}{2 m}$ 的速度从 $O$ 点沿 $z$ 轴正方向第一次穿过 $x O y$ 面进入磁场 $\mathrm{I}$, 求第四次穿过 $x O y$ 平面的 位置坐标 (用 $d$ 表示);
(4) 当离子甲以 $\frac{q B d}{2 m}$ 的速度从 $O$ 点进入磁场 $\mathrm{I}$ 时, 质量为 $4 m$ 、带电量为 $+q$ 的离子乙, 也从 $O$ 点沿 $z$ 轴 正方向以相同的动能同时进入磁场 $\mathrm{I}$, 求两离子进入磁场后, 到达它们运动轨迹第一个交点的时间差 $\Delta t$ (忽略离子间相互作用)。