在天宫课堂中、我国航天员演示了利用牛顿第二定律测量物体质量的实验。受此启发。某同学利用气垫导轨、力传感器、无线加速度传感器、轻弹簧和待测物体等器材设计了测量物体质量的实验，如图甲所示。主要步骤如下：
①将力传感器固定在气垫导轨左端支架上，加速度传感器固定在滑块上；
②接通气源。放上滑块。调平气垫导轨；

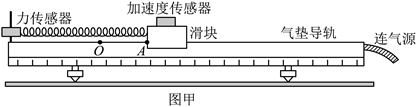
③将弹簧左端连接力传感器，右端连接滑块。弹簧处于原长时滑块左端位于O点。A点到O点的距离为5.00cm，拉动滑块使其左端处于A点，由静止释放并开始计时；
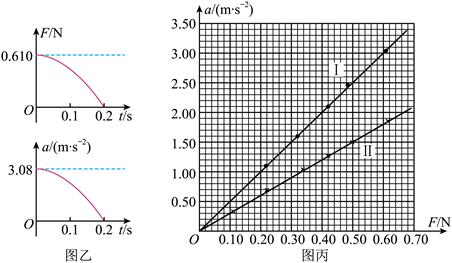
④计算机采集获取数据，得到滑块所受弹力F、加速度a随时间t变化的图像，部分图像如图乙所示。


回答以下问题（结果均保留两位有效数字）：
（1）弹簧的劲度系数为 ________ N/m。
（2）该同学从图乙中提取某些时刻F与a的数据，画出a—F图像如图丙中I所示，由此可得滑块与加速度传感器的总质量为 ________ kg。
（3）该同学在滑块上增加待测物体，重复上述实验步骤，在图丙中画出新的a—F图像Ⅱ，则待测物体的质量为 ________。