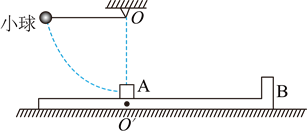
如图所示, “L” 型平板 B 静置在地面上, 小物块 A 处于平板 B 上的 $O^{\prime}$ 点, $O^{\prime}$ 点左侧粗粘, 右侧光滑。 用不可伸长的轻绳将质量为 $M$ 的小球悬挂在 $O^{\prime}$ 点正上方的 $O$ 点, 轻绳处于水平拉直状态。将小球由静止 释放, 下摆至最低点与小物块 $\mathrm{A}$ 发生碰撞, 碰后小球速度方向与碰前方向相同, 开始做简谐运动（要求摆 角小于 $\left.5^{\circ}\right), \mathrm{A}$ 以速度 $v_0$ 沿平板滑动直至与 $\mathrm{B}$ 右侧挡板发生弹性碰撞。一段时间后, $\mathrm{A}$ 返回到 $O$ 点的正下 方时, 相对于地面的速度减为零, 此时小球恰好第一次上升到最高点。已知 $\mathrm{A}$ 的质量 $m_{\mathrm{A}}=0.1 \mathrm{~kg}, \mathrm{~B}$ 的 质量 $m_{\mathrm{B}}=0.3 \mathrm{~kg}, \mathrm{~A}$ 与 $\mathrm{B}$ 的动摩擦因数 $\mu_1=0.4, \mathrm{~B}$ 与地面间的动摩擦因数 $\mu_2=0.225, v_0=4 \mathrm{~m} / \mathrm{s}$, 取 重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。整个过程中 $\mathrm{A}$ 始终在 $\mathrm{B}$ 上, 所有碰撞时间忽略不计, 不计空气阻力, 求:
(1) $\mathrm{A}$ 与 $\mathrm{B}$ 的挡板碰撞后, 二者的速度大小 $v_{\mathrm{A}}$ 与 $v_{\mathrm{B}}$;
(2) B 光滑部分的长度 $d$;
(3) 运动过程中 $\mathrm{A}$ 对 $\mathrm{B}$ 的摩擦力所做的功 $W_{\mathrm{f}}$;
(4) 实现上述运动过程, $\frac{M}{m_{\mathrm{A}}}$ 的取值范围 (结果用 $\cos 5^{\circ}$ 表示)。