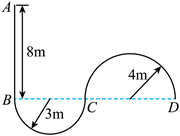
无人配送小车某次性能测试路径如图所示, 半径为 $3 \mathrm{~m}$ 的半圆弧 $B C$ 与长 $8 \mathrm{~m}$ 的直线路径 $A B$ 相切于 $B$ 点, 与半径为 $4 \mathrm{~m}$ 的半圆弧 $C D$ 相切于 $C$ 点。小车以最大速度从 $A$ 点驶入路径, 到适当位置调整速率运动 到 $B$ 点, 然后保持速率不变依次经过 $B C$ 和 $C D$ 。为保证安全, 小车速率最大为 $4 \mathrm{~m} / \mathrm{s}$ 。在 $A B C$ 段的加速 度最大为 $2 \mathrm{~m} / \mathrm{s}^2, C D$ 段的加速度最大为 $1 \mathrm{~m} / \mathrm{s}^2$ 。小车视为质点, 小车从 $A$ 到 $D$ 所需最短时间 $t$ 及在 $A B$ 段做匀速直线运动的最长距离 $l$ 为
$\text{A.}$ $t=\left(2+\frac{7 \pi}{4}\right) \mathrm{s}, l=8 \mathrm{~m}$
$\text{B.}$ $t=\left(\frac{9}{4}+\frac{7 \pi}{2}\right) \mathrm{s}, l=5 \mathrm{~m}$.
$\text{C.}$ $t=\left(2+\frac{5}{12} \sqrt{6}+\frac{7 \sqrt{6} \pi}{6}\right) \mathrm{s}, l=5.5 \mathrm{~m}$.
$\text{D.}$ $t=\left[2+\frac{5}{12} \sqrt{6}+\frac{(\sqrt{6}+4) \pi}{2}\right] \mathrm{s}, l=5.5 \mathrm{~m}$