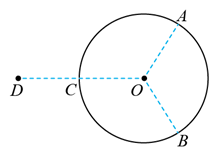
半径为 $R$ 的绝缘细圆环固定在图示位置, 圆心位于 $O$ 点, 环上均匀份布着电量为 $Q$ 的正电荷。点 $A 、 B 、$ $C$ 将圆环三等分, 取走 $A 、 B$ 处两段弧长均为 $\Delta L$ 的小圆弧上的电荷。将一点电荷 $q$ 置于 $O C$ 延长线上距 $O$ 点为 $2 R$ 的 $D$ 点, $O$ 点的电场强度刚好为零。圆环上剩余电荷分布不变, $q$ 为
$\text{A.}$ 正电荷, $q=\frac{Q \Delta L}{\pi R}$
$\text{B.}$ 正电荷, $q=\frac{\sqrt{3} Q \Delta L}{\pi R}$
$\text{C.}$ 负电荷, $q=\frac{2 Q \Delta L}{\pi R}$
$\text{D.}$ 负电荷, $q=\frac{2 \sqrt{3} Q \Delta L}{\pi R}$