单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\{1,2,3,4,5\}, B=\{(x, y) \mid x \in A, y \in A, x-y \in A\}$, 则 B 中所含元素的个数为()
$\text{A.}$ 3
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 10
将 2 名教师, 4 名学生分成 2 个小组, 分别安排到甲、乙两地参加社会实践活动, 每个小组由 1 名教师和 2 名学生组成, 不同的安排方案共有 ( )
$\text{A.}$ 12 种
$\text{B.}$ 10 种
$\text{C.}$ 9 种
$\text{D.}$ 18种
下面是关于复数 $z=\frac{2}{-1+i}$ 的四个命题: 其中的真命题为 ( )
$p_{1}:|z|=2$,
$\mathrm{p}_{2}: \mathrm{z}^{2}=2 \mathrm{i}$,
$p_{3}$ : $z$ 的共轭复数为 $1+\mathrm{i}$,
$\mathrm{p}_{4}$ : $\mathrm{z}$ 的虚部为 $-1 .$
$\text{A.}$ $\mathrm{p}_{2}, \mathrm{p}_{3}$
$\text{B.}$ $\mathrm{p}_{1}, \mathrm{p}_{2}$
$\text{C.}$ $\mathrm{p}_{2}, \mathrm{p}_{4}$
$\text{D.}$ $\mathrm{p}_{3}, \mathrm{p}_{4}$
设 $F_{1} 、 F_{2}$ 是椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左、右焦点, $P$ 为直线 $x=$ $\frac{3 \mathrm{a}}{2}$ 上一点, $\triangle \mathrm{F}_{2} P F_{1}$ 是底角为 $30^{\circ}$ 的等腰三角形, 则 $\mathrm{E}$ 的离心率为( )
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{4}{5}$
已知 $\left\{a_{n}\right\}$ 为等比数列, $a_{4}+a_{7}=2, a_{5} a_{6}=-8$, 则 $a_{1}+a_{10}=$ ( )
$\text{A.}$ 7
$\text{B.}$ 5
$\text{C.}$ $-5$
$\text{D.}$ $-7$
如果执行右边的程序框图, 输入正整数 $N(N \geqslant 2)$ 和实数 $a_{1}, a_{2}, \ldots$ , $a_{n}$, 输出 $A, B$, 则 ( )
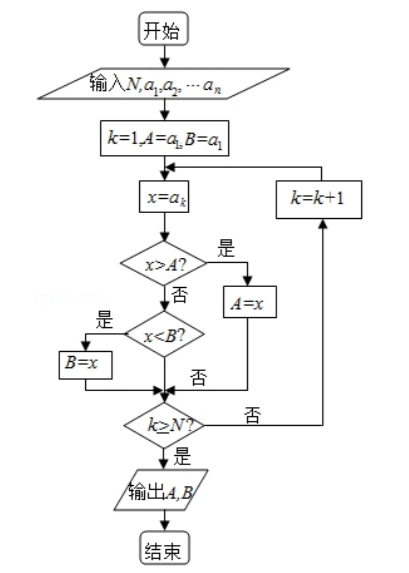
$\text{A.}$ $A+B$ 为 $a_{1}, a_{2}, \ldots, a_{n}$ 的和
$\text{B.}$ $\frac{A+B}{2}$ 为 $a_{1}, a_{2}, \ldots, a_{n}$ 的算术平均数
$\text{C.}$ $A$ 和 $B$ 分别是 $a_{1}, a_{2}, \ldots, a_{n}$ 中最大的数和最小的数
$\text{D.}$ $A$ 和 $B$ 分别是 $a_{1}, a_{2}, \ldots, a_{n}$ 中最小的数和最大的数
如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
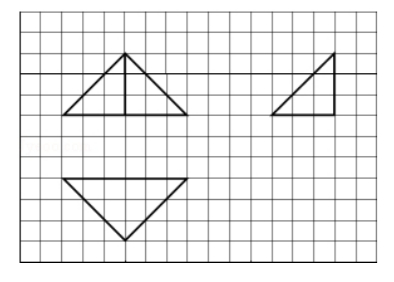
$\text{A.}$ 6
$\text{B.}$ 9
$\text{C.}$ 12
$\text{D.}$ 18
等轴双曲线 $C$ 的中心在原点, 焦点在 $x$ 轴上, $C$ 与抛物线 $y^{2}=16 x$ 的 准线交于点 $A$ 和点 $B,|A B|=4 \sqrt{3}$, 则 $C$ 的实轴长为 ( )
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 4
$\text{D.}$ 8
已知 $\omega>0$, 函数 $f(x)=\sin \left(\omega x+\frac{\pi}{4}\right)$ 在区间 $\left[\frac{\pi}{2}, \pi\right]$ 上单调递减, 则实数 $\omega$ 的取值范围是 ( )
$\text{A.}$ $\left[\frac{1}{2}, \frac{5}{4}\right]$
$\text{B.}$ $\left[\frac{1}{2}, \frac{3}{4}\right]$
$\text{C.}$ $\left(0, \frac{1}{2}\right]$
$\text{D.}$ $(0,2]$
已知函数 $f(x)=\frac{1}{\ln (x+1)-x}$, 则 $\mathrm{y}=\mathrm{f}(\mathrm{x})$ 的图象大致为 ( )
$\text{A.}$ 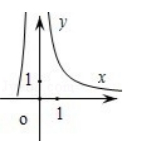 $\text{B.}$
$\text{B.}$ 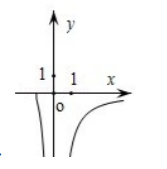 $\text{C.}$
$\text{C.}$ 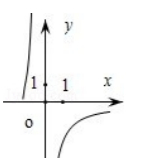 $\text{D.}$
$\text{D.}$ 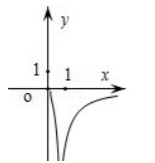
已知三棱雉 S- $A B C$ 的所有顶点都在球 $O$ 的表面上, $\triangle A B C$ 是边长 为 1 的正三角形, $S C$ 为球 $O$ 的直径, 且 $S C=2$, 则此三棱雉的体积为 ( )
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{\sqrt{2}}{4}$
$\text{C.}$ $\frac{\sqrt{2}}{6}$
$\text{D.}$ $\frac{\sqrt{2}}{12}$
设点 $P$ 在曲线 $y=\frac{1}{2} e^{x}$ 上, 点 $Q$ 在曲线 $y=\ln (2 x)$ 上, 则 $|P Q|$ 最小 值为 ( )
$\text{A.}$ $1-\ln 2$
$\text{B.}$ $\sqrt{2}(1-\ln 2)$
$\text{C.}$ $1+\ln 2$
$\text{D.}$ $\sqrt{2}(1+\ln 2)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $\vec{a}, \overrightarrow{\mathrm{b}}$ 大角为 $45^{\circ}$, 且 $|\overrightarrow{\mathrm{a}}|=1,|2 \vec{a}-\vec{b}|=\sqrt{10}$, 则 $|\vec{b}|=$
设 $x, y$ 满足约束条件: $\left\{\begin{array}{l}x \geqslant 0, y \geqslant 0 \\ x-y \geqslant-1 \\ x+y \leqslant 3\end{array}\right.$; 则 $z=x-2 y$ 的取值范围为
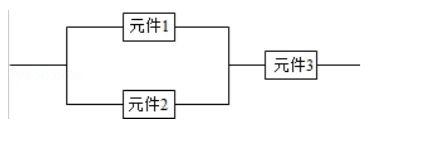
某个部件由三个元件按下图方式连接而成, 元件 1 或元件 2 正常工 作, 且元件 3 正常工作, 则部件正常工作, 设三个电子元件的使用寿命(单 位:小时) 均服从正态分布 $N\left(1000,50^{2}\right)$, 且各个元件能否正常相互独立, 那么该部件的使用寿命超过 1000 小时的概率为
数列 $\left\{a_{n}\right\}$ 满足 $a_{n+1}+(-1)^{n} a_{n}=2 n-1$, 则 $\left\{a_{n}\right\}$ 的前 60 项和为
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $a, b, c$ 分别为 $\triangle A B C$ 三个内角 $A, B, C$ 的对边, $a \cos C+\sqrt{3} a \sin C-b-c=0$
(1) 求 $A$;
(2)若 $a=2, \triangle A B C$ 的面积为 $\sqrt{3}$; 求 $b, c$.
某花店每天以每枝 5 元的价格从农场购进若干枝玫瑰花, 然后以 每枝 10 元的价格出售, 如果当天卖不完, 剩下的玫瑰花作垃圾处理.
(1)若花店一天购进 16 枝玫瑰花, 求当天的利润 y(单位: 元)关于当天需求 量 $\mathrm{n}$ (单位: 枝, $\mathrm{n} \in \mathrm{N}$ ) 的函数解析式.
(2)花店记录了 100 天玫瑰花的日需求量(单位:枝),整理得如表:

以 100 天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进 16 枝玫瑰花, $\mathrm{X}$ 表示当天的利润(单位:元), 求 $\mathrm{X}$ 的分 布列、数学期望及方差;
(ii)若花店计划一天购进 16 枝或 17 枝玫瑰花, 你认为应购进 16 枝还是 17 枝
? 请说明理由.
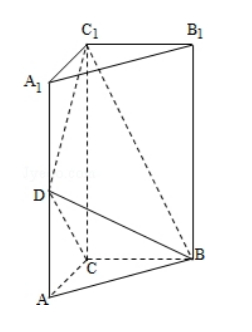
如图, 直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 中, $A C=B C=\frac{1}{2} A A_{1}, D$ 是棱 $A A_{1}$ 的中 点, $D C_{1} \perp B D$
(1) 证明: $D C_{1} \perp B C$;
(2) 求二面角 $A_{1}-B D-C_{1}$ 的大小.
设抛物线 $C: x^{2}=2 p y(p>0)$ 的焦点为 $F$, 准线为 $I, A \in C$, 已知以 $F$ 为圆心, $F A$ 为半径的圆 $F$ 交 I 于 $B, D$ 两点;
(1) 若 $\angle B F D=90^{\circ}, \triangle A B D$ 的面积为 $4 \sqrt{2}$, 求 $p$ 的值及圆 $F$ 的方程;
(2) 若 $\mathrm{A}, \mathrm{B}, \mathrm{F}$ 三点在同一直线 $\mathrm{m}$ 上, 直线 $\mathrm{n}$ 与 $\mathrm{m}$ 平行, 且 $\mathrm{n}$ 与 $\mathrm{C}$ 只有一个 公共点, 求坐标原点到 $m, n$ 距离的比值.
已知函数 $f(x)$ 满足 $f(x)=f^{\prime}$ (1) $e^{x-1}-f(0) x+\frac{1}{2} x^{2}$;
(1)求 $f(x)$ 的解析式及单调区间;
(2) 若 $f(x) \geqslant \frac{1}{2} x^{2}+a x+b$, 求 $(a+1) b$ 的最大值.
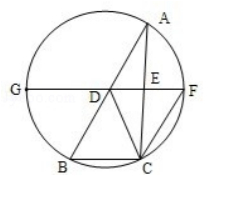
如图, $D, E$ 分别为 $\triangle A B C$ 边 $A B, A C$ 的中点, 直线 $D E$ 交 $\triangle A B C$ 的 外接圆于 $F, G$ 两点, 若 $C F / / A B$, 证明:
(1) $C D=B C$;
(2) $\triangle B C D \sim \triangle G B D$.
已知曲线 $C_{1}$ 的参数方程是 $\left\{\begin{array}{l}x=2 \cos \phi \\ y=3 \sin \phi\end{array}\right.$ ( $\phi$ 为参数), 以坐标原点为极点, $x$ 轴的 正半轴为极轴建立坐标系, 曲线 $C_{2}$ 的坐标系方程是 $\rho=2$, 正方形 $A B C D$ 的顶
点都在 $C_{2}$ 上, 且 $A, B, C, D$ 依逆时针次序排列, 点 $A$ 的极坐标为 $\left(2, \frac{\pi}{3}\right)$
(1) 求点 $A, B, C, D$ 的直角坐标;
(2)设 $P$ 为 $C_{1}$ 上任意一点, 求 $|P A|^{2}+|P B|^{2}+|P C|^{2}+|P D|^{2}$ 的取值范围.
已知函数 $f(x)=|x+a|+|x-2|$
(1)当 $a=-3$ 时, 求不等式 $f(x) \geqslant 3$ 的解集;
(2) $f(x) \leqslant|x-4|$ 若的解集包含 $[1,2]$, 求 $a$ 的取值范围.