单选题 （共 8 题 ），每题只有一个选项正确
设复数 $z=i(2-3 i)$, 则 $|z|=$
$\text{A.}$ $\sqrt{13}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $3$
$\text{D.}$ $5$
已知集合 $A=\{0,1,2\}, B=\{x \in N \mid-2 < x < 3\}$, 则 $A \cup B=$
$\text{A.}$ $\{0,1\}$
$\text{B.}$ $\{1,2\}$
$\text{C.}$ $\{0,1,2\}$
$\text{D.}$ $\{-1,0,1,2\}$
已知命题 $p: \exists x \in N, e^x < 0$ ( $e$ 为自然对数的底数)； $q: \forall x \in R, x^2+|x| \geqslant 0$ ，则下 列为真命题的是
$\text{A.}$ $p$ 真, $q$ 假
$\text{B.}$ $p$ 真, $q$ 真
$\text{C.}$ $p$ 假, $q$ 真
$\text{D.}$ $p$ 假, $q$ 假
已知平面向量 $\vec{a}, \vec{b}$ 满足 $\vec{a}=(1,-\sqrt{3}),|\vec{b}|=1,|\vec{a}+2 \vec{b}|=2$, 则向量 $\vec{a}$ 与向量 $\vec{a}+2 \vec{b}$ 的夹角为
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{\pi}{2}$
函数 $f(x)=\frac{e \ln x^2}{2 x}$ 的图象大致是
$\text{A.}$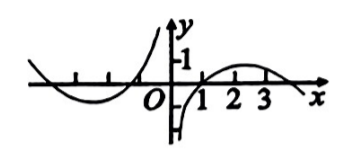 
$\text{B.}$ 
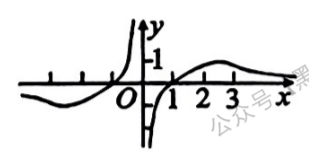$\text{C.}$ 
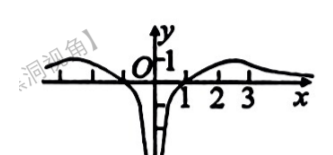$\text{D.}$ 
现将甲乙丙丁四个人全部安排到 $A$ 市、 $B$ 市、 $C$ 市三个地区工作, 要求每个地区都有 人去, 则甲乙两个人至少有一人到 $A$ 市工作的安排种数为
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 18
$\text{D.}$ 22
已知数列, $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $3 a_2=a_1+8, S_n=a_{n+1}-2$, 则 $S_{2022}=$
$\text{A.}$ $2^{2021}-1$
$\text{B.}$ $2^{2022}-1$
$\text{C.}$ $3 \times 2^{2021}-2$
$\text{D.}$ $3 \times 2^{2022}-2$
已知抛物线 $E: y^2=4 x$ 的焦点为 $F$, 准线 $l$ 交 $x$ 轴于点 $H$, 过点 $H$ 的直线与抛物线交于 $A, B$ 两点, 且 $\overrightarrow{H A}=3 \overrightarrow{H B}$, 则 $|\overrightarrow{F A}|=$
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $4$
$\text{C.}$ $4 \sqrt{3}$
$\text{D.}$ $8$
多选题 （共 4 题 ），每题有多个选项正确
在回归分析中, 下列说法正确的是
$\text{A.}$ 相关系数 $0 < r < 1$, 表示变是 $x, y$ 之间具有正相关关系
$\text{B.}$ 相关系数 $r$ 的绝对值越接近 1, 说明相关性越弱
$\text{C.}$ 点 $\left(x_i, y_i\right)$ 所对应的残差是指 $y_i-\hat{y}_i$
$\text{D.}$ $R^2$ 越大, 说明残差的平方和越小, 即模型的拟合效果越好
已知函数 $f(x)=A \sin (\omega x-\varphi)\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的部分图象如图所示, 且过点 $(0,1)$, 若存在使 $g(x)=f(x-a)$ 为奇函数成立的实数 $a$, 则 $|a|$ 可能取值为
$\text{A.}$ $\frac{\pi}{3}$
$\text{B.}$ $\frac{5 \pi}{12}$
$\text{C.}$ $\frac{\pi}{6}$
$\text{D.}$ $\frac{\pi}{12}$
数列 $\left\{a_n\right\}$ 满足 $a_1=-21, a_2=-12, a_{n+1}+a_{n-1}=2 a_n-2(n \geqslant 2), S_n$ 是 $\left\{a_n\right\}$ 的前 $n$ 项 和, 则下列说法正确的是
$\text{A.}$ $\left\{\frac{a_n}{n-8}\right\}$ 是等差数列
$\text{B.}$ $a_n=-n^2+12 n+32$
$\text{C.}$ $a_6$ 是数列 $\left\{a_n\right\}$ 的最大项
$\text{D.}$ 对于两个正整数 $m 、 n(n>m), S_n-S_m$ 的最大值为 10
已知函数 $f(x)=e^x-\ln (x+m)$, 则下面对函数 $f(x)$ 的描述正确的是
$\text{A.}$ 当 $m=0$ 时, $f(x) < 0$ 无解
$\text{B.}$ 当 $m=3$ 时, $f(x)>-\frac{1}{2}$ 恒成立
$\text{C.}$ 当 $m=3$ 时, $f(x)=-1$ 有解
$\text{D.}$ 当 $m=2$ 时, $f(x)>0$ 恒成立
填空题 （共 4 题 ），请把答案直接填写在答题纸上
在 $\left(\sqrt{x}-\frac{1}{x}\right)^6$ 的展开式中, $x^3$ 的系数为
已知实数 $a, b>0$, 若 $a+2 b=1$, 则 $\frac{3}{b}+\frac{1}{a}$ 的最小值为
已知 $\triangle A B C$ 中, $A B=A C=2, B C=2 \sqrt{2}, A D$ 为 $B C$ 边上的高线, 以 $A D$ 为折痕进行折
叠, 使得二面角 $B-A D-C$ 为 $\frac{2 \pi}{3}$, 则三棱雉 $A-B C D$ 的外接球半径为
已知定义在 $R$ 上的函数 $f(x)$ 满足 $f(x)=2 f(x-2)$, 当 $x \in[-1,1)$ 时,$f(x)=2^{|x|}-\frac{3}{2}$. 若 $g(x)=\log _2 x, \exists a \in[3,5)$, 且对 $\forall b$ 都满足 $f(a)=g(b)$, 则 $b$的取值范围是
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\sin 2 x+2 \sin ^2 x+2$.
(1) 求 $f(x)$ 的最小正周期及值域;
（2）求 $f(x)$ 的单调递增区间.
某电影院对观众按照性别进行了分层抽样调查, 一共调查了 900 名观众对 $A$ 影片和 $B$ 影片的喜爱度, 获得了以下数据:
（1）哪个影片更受学生欢迎? (不用说明理由)
（2）分别估计该电影院男观众和女观众对 $B$ 影片表示 “非常喜爱” 的概率;
(3) 该电影院为了进一步调查观众对 $B$ 影片的看法, 对样本中的女观众用分层抽样抽 取了 6 人, 再从这 6 人中随机抽取 2 人参加座谈, 求这两人均来自 “一般喜爱” 群体的概率.
在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别为 $a, b, c$. 已知 $(b-a)\left[\sin (B+C)+\sin \left(A^{\prime}+C\right)\right]=\sin C(a+c)$.
(1) 求 $B$;
(2) 若 $\angle A B C$ 的平分线交 $A C$ 于点 $D$, 且 $B D=2$, 求 $b$ 的最小值.
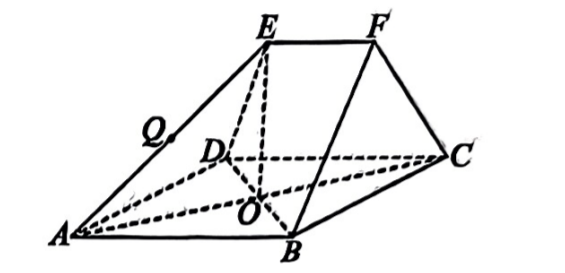
如图, 在多面体 $A B C D E F$ 中, 四边形 $A B C D$ 是边长为 4 的菱形, $\angle B C D=60^{\circ}, A C$ 与 $B D$ 交于点 $O$, 平面 $F B C \perp$ 平面 $A B C D, E F / / A B, F B=F C, E F=2$.
(1) 求证: $O E \perp$ 平面 $A B C D$;
(2) 若 $A E \perp F C$, 点 $Q$ 为 $A E$ 的中点, 求二面角 $Q-B C-A$ 的余弦值.
已知椭圆 $C: \frac{x^2}{4}+\frac{y^2}{2}=1$ 的上、下顶点分别为 $A_1 、 A_2$, 点 $P$ 是椭圆 $C$ 上异于 $A_1 、 A_2$ 的 动点, 记 $k_1, k_2$ 分别为直线 $P A_1, P A_2$ 的斜率. 点 $Q$ 满足 $Q A_1 \perp P A_1, Q A_2 \perp P A_2$.
（1）证明： $k_1 k_2$ 是定值, 并求出该定值;
(2) 求动点 $Q$ 的轨迹方程.
已知函数 $f(x)=\frac{1}{2} x^2+a x-2 a^2 \ln x$.
（1）讨论函数 $f(x)$ 的单调性;
(2) 若 $a>0, x_1, x_2$ 是 $f(x)$ 的两个不相等的零点, 证明: $f^{\prime}\left(\frac{x_1+x_2}{2}\right)>0$.