单选题 (共 8 题 ),每题只有一个选项正确
设 $z=1+\mathrm{i}$ ,则 $z^2-\mathrm{i}=$
$\text{A.}$ $i$
$\text{B.}$ $-{i}$
$\text{C.}$ $1$
$\text{D.}$ $-1$
设集合 $A=\left\{2,3, a^2-2 a-3\right\} , B=\{0,3\} , C=\{2, a\}$. 若 $B \subseteq A , A \cap C=\{2\}$ ,则 $a=$
$\text{A.}$ $-3$
$\text{B.}$ $-1$
$\text{C.}$ $1$
$\text{D.}$ $3$
甲、乙、丙、丁四名教师带领学生参加校园植树活动,教师随机分成三组,每组至少一人, 则甲、乙在同一组的概率为
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
平面向量 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 相互垂直,已知 $\boldsymbol{a}=(6,-8) ,|\boldsymbol{b}|=5$ , 且 $\boldsymbol{b}$ 与向量 $(1,0)$ 的夹角是钝角,则$b=$
$\text{A.}$ $(-3,-4)$
$\text{B.}$ $(4,3)$
$\text{C.}$ $(-4,3)$
$\text{D.}$ $(-4,-3)$
已知点 $A, B, C$ 为椭圆 $D$ 的三个顶点,若 $\triangle A B C$ 是正三角形,则 $D$ 的离心率是
$\text{A.}$ $\cdot \frac{1}{2}$
$\text{B.}$ $\cdot \frac{2}{3}$
$\text{C.}$ $\frac{\sqrt{6}}{3}$
$\text{D.}$ $\frac{\sqrt{3}}{2}$
三棱椎 $A-B C D$ 中, $A C \perp$ 平面 $B C D , B D \perp C D$. 若 $A B=3 , B D=1$ ,则该三棱雉体 积的最大值为
$\text{A.}$ $2$
$\text{B.}$ $\frac{4}{3}$
$\text{C.}$ $1$
$\text{D.}$ $\frac{2}{3}$
设函数 $f(x) , g(x)$ 在 $\mathbf{R}$ 的导函数存在,且 $f^{\prime}(x) < g^{\prime}(x)$ ,则当 $x \in(a, b)$ 时
$\text{A.}$ $f(x) < g(x)$
$\text{B.}$ $f(x)>g(x)$
$\text{C.}$ $f(x)+g(a) < g(x)+f(a)$
$\text{D.}$ $f(x)+g(b) < g(x)+f(b)$
已知 $a , b , c$ 满足 $a=\log _5\left(2^b+3^b\right) , c=\log _3\left(5^b-2^b\right)$ ,则
$\text{A.}$ $|a-c| \geq|b-c|,|a-b| \geq|b-c|$
$\text{B.}$ $|a-c| \geq|b-c|,|a-b| \leq|b-c|$
$\text{C.}$ $|a-c| \leq|b-c|,|a-b| \geq|b-c|$
$\text{D.}$ $|a-c| \leq|b-c|,|a-b| \leq|b-c|$
多选题 (共 4 题 ),每题有多个选项正确
.已知 $f(x)$ 是定义在 $\mathbf{R}$ 上的偶函数 , $g(x)$ 是定义在 $\mathbf{R}$ 上的奇函数 ,且 $f(x) , g(x)$ 在 $(-\infty, 0]$ 单调递减,则
$\text{A.}$ $f(f(1)) < f(f(2))$
$\text{B.}$ $f(g(1)) < f(g(2))$
$\text{C.}$ $g(f(1)) < g(f(2))$
$\text{D.}$ $g(g(1)) < g(g(2))$
已知平面 $\alpha \cap$ 平面 $\beta=l, B, D$ 是 $l$ 上两点,直线 $A B \subset \alpha$ 且 $A B \cap l=B$ ,直线 $C D \subset \beta$ 且 $C D \cap l=D$. 下列结论中,错误的有
$\text{A.}$ 若 $A B \perp l , C D \perp l$ ,且 $A B=C D$ ,则 $A B C D$ 是平行四边形
$\text{B.}$ 若 $M$ 是 $A B$ 中点, $N$ 是 $C D$ 中点,则 $M N / / A C$
$\text{C.}$ 若 $\alpha \perp \beta , A B \perp l , A C \perp l$ ,则 $C D$ 在 $\alpha$ 上的射影是 $B D$
$\text{D.}$ 直线 $A B , C D$ 所成角的大小与二面角 $\alpha-l-\beta$ 的大小相等
质点 $P$ 和 $Q$ 在以坐标原点 $O$ 为圆心,半径为 1 的 $\odot O$ 上逆时针作匀速圆周运动,同时出 发. $P$ 的角速度大小为 $2 \mathrm{rad} / \mathrm{s}$ ,起点为 $\odot O$ 与 $x$ 轴正半轴的交点; $Q$ 的角速度大小为 $5 \mathrm{rad} / \mathrm{s}$ , 起点为射线 $y=-\sqrt{3} x(x \geq 0)$ 与 $\odot O$ 的交点,则当 $Q$ 与 $P$ 重合时, $Q$ 的坐标可以为
$\text{A.}$ $\left(\cos \frac{2 \pi}{9}, \sin \frac{2 \pi}{9}\right)$
$\text{B.}$ $\left(-\cos \frac{5 \pi}{9},-\sin \frac{5 \pi}{9}\right)$
$\text{C.}$ $\left(\cos \frac{\pi}{9},-\sin \frac{\pi}{9}\right)$
$\text{D.}$ $\left(-\cos \frac{\pi}{9}, \sin \frac{\pi}{9}\right)$
下图改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时 历》时所做的天文计算. 图中的 $\overparen{A B} , \overparen{A C} , \overparen{B D} , \overparen{C D}$ 都是以 $O$ 为圆心的圆弧,CMNK 是为 计算所做的矩形,其中 $M, N, K$ 分别在线段 $O D, O B, O A$ 上, $M N \perp O B, K N \perp O B$. 记 $\alpha=\angle A O B , \beta=\angle A O C , \gamma=\angle B O D , \delta=\angle C O D$ ,则
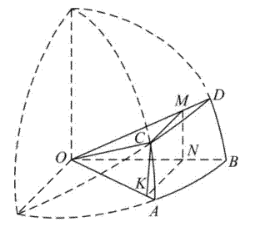
$\text{A.}$ $\sin \beta=\sin \gamma \cos \delta$
$\text{B.}$ $\cos \beta=\cos \gamma \cos \delta$
$\text{C.}$ $\sin \alpha=\frac{\sin \delta}{\cos \beta}$
$\text{D.}$ $\cos \alpha=\frac{\cos \gamma \cos \delta}{\cos \beta}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
. 某工厂生产的产品的质量指标服从正态分布 $N\left(100, \sigma^2\right)$. 质量指标介于 99 至 101 之间的产 品为良品,为使这种产品的良品率达到 $95.45 \%$ ,则需调整生产工艺,使得 $\sigma$ 至多为
(若 $X \sim N\left(\mu, \sigma^2\right)$ ,则 $P\{|X-\mu| < 2 \sigma\}=0.9545$ )
若 $P , Q$ 分别是抛物线 $x^2=y$ 与圆 $(x-3)^2+y^2=1$ 上的点,则 $|P Q|$ 的最小值为
数学家祖冲之曾给出圆周率 $\pi$ 的两个近似值 : "约率" $\frac{22}{7}$ 与 “密度" $\frac{355}{113}$. 它们可用 “调日法" 得到:称小于 $3.1415926$ 的近似值为弱率,大于 $3.1415927$ 的近似值为强率. 由 $\frac{3}{1} < \pi < \frac{4}{1}$ ,取 3 为弱率, 4 为强率,得 $a_1=\frac{3+4}{1+1}=\frac{7}{2}$ ,故 $a_1$ 为强率;与上一次的弱率 3 计算 得 $a_2=\frac{3+7}{1+2}=\frac{10}{3}$ ,故 $a_2$ 为强率,继续计算, $\cdots \cdots$. 若某次得到的近似值为强率,与上一次 的弱率继续计算得到新的近似值;若某次得到的近似值为弱率,与上一次的强率继续计算得到 新的近似值,依此类推.已知 $a_m=\frac{22}{7}$ ,则 $m=$ $a_8=$
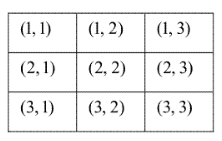
. 下图为一个开关阵列,每个开关只有 "开" 和 "关" 两种状态,按其中一个开关 1 次,将 导致自身和所有相邻的开关改变状态.例如,按 $(2,2)$ 将导致(1,2),(2,1),(2,2),(2,3),(3,2)
改变状态如果要求只改变 $(1,1)$ 的状态,则需按开关的最少次数为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
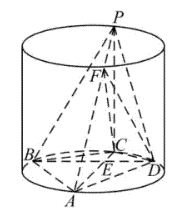
如图,四边形 $A B C D$ 是圆柱底面的内接四边形, $A C$ 是圆柱的底面直径, $P C$ 是 圆柱的母线, $E$ 是 $A C$ 与 $B D$ 的交点, $A B=A D, \angle B A D=60^{\circ}$.
(1) 记圆柱的体积为 $V_1$ ,四棱雉 $P-A B C D$ 的体积为 $V_2$ ,求 $\frac{V_1}{V_2}$ ;
(2)设点 $F$ 在线段 $A P$ 上, $P A=4 P F , P C=4 C E$ ,求二面角 $F-C D-P$ 的余弦值.
已知函数 $f(x)=\sin (\omega x+\varphi)$ 在区间 $\left(\frac{\pi}{6}, \frac{\pi}{2}\right)$ 单调,其中 $\omega$ 为正整数, $|\varphi| < \frac{\pi}{2}$ , 且 $f\left(\frac{\pi}{2}\right)=f\left(\frac{2 \pi}{3}\right)$.
(1) 求 $y=f(x)$ 图像的一条对称轴;
(2) 若 $f\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}$ ,求 $\varphi$.
设数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $T_n$ ,且 $a_1=1 , a_n=T_{n-1}(n \geq 2)$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2)设 $m$ 为整数,且对任意 $n \in \mathbf{N}^* , m \geq \frac{1}{a_1}+\frac{2}{a_2}+\cdots+\frac{n}{a_n}$ ,求 $m$ 的最小值.
一个池塘里的鱼的数目记为 $N$ ,从池塘里捞出 200 尾鱼,并给鱼作上标识,然后 把鱼放回池塘里,过一小段时间后再从池塘里捞出 500 尾鱼, $X$ 表示捞出的 500 尾鱼中有标 识的鱼的数目.
(1)若 $N=5000$ ,求 $X$ 的数学期望;
(2 )已知捞出的 500 尾鱼中 15 尾有标识,试给出 $N$ 的估计值 ( 以使得 $P(X=15)$ 最大的 $N$ 的 值作为 $N$ 的估计值 ).
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 过点 $A(4 \sqrt{2}, 3)$ ,且焦距为 10 .
(1) 求 $C$ 的方程 ;
(2) 已知点 $B(4 \sqrt{2},-3) , D(2 \sqrt{2}, 0) , E$ 为线段 $A B$ 上一点,且直线 $D E$ 交 $C$ 于 $G , H$ 两
点.证明 : $\frac{|G D|}{|G E|}=\frac{|H D|}{|H E|}$.
椭圆曲线加密算法运用于区块链
椭圆曲线 $C=\left\{(x, y) \mid y^2=x^3+a x+b, 4 a^3+27 b^2 \neq 0\right\} . P \in C$ 关于 $x$ 轴的对称点记为 $\tilde{P} . C$
在点 $P(x, y)(y \neq 0)$ 处的切线是指曲线 $y=\pm \sqrt{x^3+a x+b}$ 在点 $P$ 处的切线定义 " $\oplus$ " 运算满 足 :
①若 $P \in C , Q \in C$, 且直线 $P Q$ 与 $C$ 有第三个交点 $R$, 则 $P \oplus Q=\tilde{R}$;
②若 $P \in C , Q \in C$ , 且 $P Q$ 为 $C$ 的切线,切点为 $P$ ,则 $P \oplus Q=\tilde{P}$ ;③若 $P \in C$ ,规定 $P \oplus \tilde{P}=0^*$ ,且 $P \oplus 0^*=0^* \oplus P=P$.
(1) 当 $4 a^3+27 b^2=0$ 时,讨论函数 $h(x)=x^3+a x+b$ 零点的个数;
(2) 已知 " $\oplus$ " 运算满足交换律、结合律,若 $P \in C , Q \in C$ ,且 $P Q$ 为 $C$ 的切线,切点为 $P$ ,证明 : $P \oplus P=\tilde{Q}$ ;
(3) 已知 $P\left(x_1, y_1\right) \in C , Q\left(x_2, y_2\right) \in C$ ,且直线 $P Q$ 与 $C$ 有第三个交点,求 $P \oplus Q$ 的坐标.
参考公式 : $m^3-n^3=(m-n)\left(m^2+m n+n^2\right)$