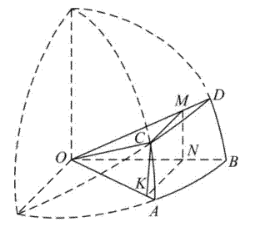
下图改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时 历》时所做的天文计算. 图中的 $\overparen{A B} , \overparen{A C} , \overparen{B D} , \overparen{C D}$ 都是以 $O$ 为圆心的圆弧,CMNK 是为 计算所做的矩形,其中 $M, N, K$ 分别在线段 $O D, O B, O A$ 上, $M N \perp O B, K N \perp O B$. 记 $\alpha=\angle A O B , \beta=\angle A O C , \gamma=\angle B O D , \delta=\angle C O D$ ,则

A. $\sin \beta=\sin \gamma \cos \delta$
B. $\cos \beta=\cos \gamma \cos \delta$
C. $\sin \alpha=\frac{\sin \delta}{\cos \beta}$
D. $\cos \alpha=\frac{\cos \gamma \cos \delta}{\cos \beta}$