单选题 （共 12 题 ），每题只有一个选项正确
函数 $y=\sqrt{x(x-1)}+\sqrt{x}$ 的定义域为（ ）
$\text{A.}$ $\{x \mid x \geqslant 0\}$
$\text{B.}$ $\{x \mid x \geqslant 1\}$
$\text{C.}$ $\{x \mid x \geqslant 1\} \cup\{0\}$
$\text{D.}$ $\{x \mid 0 \leqslant x \leqslant 1\}$
汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车, 若把这 一过程中汽车的行驶路程 $\mathrm{s}$ 看作时间 $\mathrm{t}$ 的函数, 其图象可能是 （ ）
$\text{A.}$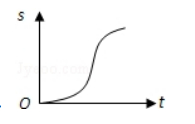 
$\text{B.}$ 
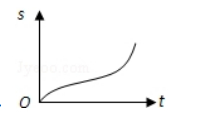$\text{C.}$ 
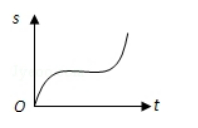$\text{D.}$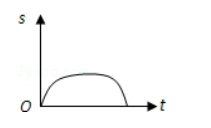 
在 $\triangle \mathrm{ABC}$ 中, $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{b}}$. 若点 $\mathrm{D}$ 满足 $\overrightarrow{\mathrm{BD}}=2 \overrightarrow{\mathrm{DC}}$, 则 $\overrightarrow{\mathrm{AD}}=($ )
$\text{A.}$ $\frac{2}{3} \overrightarrow{\mathrm{b}}+\frac{1}{3} \overrightarrow{\mathrm{c}}$
$\text{B.}$ $\frac{5}{3} \vec{c}-\frac{2}{3} \vec{b}$
$\text{C.}$ $\frac{2}{3} \vec{b}-\frac{1}{3} \vec{c}$
$\text{D.}$ $\frac{1}{3} \vec{b}+\frac{2}{3} \vec{c}$
设 $\mathrm{a} \in \mathrm{R}$, 且 $(\mathrm{a}+\mathrm{i})^{2} \mathrm{i}$ 为正实数, 则 $\mathrm{a}=$ （ ）
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ 0
$\text{D.}$ -1
已知等差数列 $\left\{a_{n}\right\}$ 满足 $a_{2}+a_{4}=4, a_{3}+a_{5}=10$, 则它的前 10 项的和 $S_{10}=$ （ ）
$\text{A.}$ 138
$\text{B.}$ 135
$\text{C.}$ 95
$\text{D.}$ 23
若函数 $y=f(x)$ 的图象与函数 $y=\ln \sqrt{x}+1$ 的图象关于直线 $y=x$ 对称, 则 $f(x)=$ （ ）
$\text{A.}$ $\mathrm{e}^{2 \mathrm{x}-2}$
$\text{B.}$ $\mathrm{e}^{2 \mathrm{x}}$
$\text{C.}$ $\mathrm{e}^{2 \mathrm{x}+1}$
$\text{D.}$ $\mathrm{e}^{2 \mathrm{x}+2}$
已知曲线 $y=\frac{x+1}{x-1}$ 在点 $(3,2$ ) 处的切线与直线 $a x+y+1=0$ 垂直, 则 $a$ 的值为 $($ )
$\text{A.}$ $2$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $-2$
为得到函数 $y=\cos \left(2 x+\frac{\pi}{3}\right)$ 的图象, 只需将函数 $y=\sin 2 x$ 的图象 ( )
$\text{A.}$ 向左平移 $\frac{5 \pi}{12}$ 个长度单位
$\text{B.}$ 向右平移 $\frac{5 \pi}{12}$ 个长度单位
$\text{C.}$ 向左平移 $\frac{5 \pi}{6}$ 个长度单位
$\text{D.}$ 向右平移 $\frac{5 \pi}{6}$ 个长度单位
设奇函数 $f(x)$ 在 $(0,+\infty)$ 上为增函数, 且 $f(1)=0$, 则不等式 $\frac{f(x)-f(-x)}{x} < 0$ 的解集为 （ ）
$\text{A.}$ $(-1,0) \cup(1,+\infty)$
$\text{B.}$ $(-\infty,-1) \cup(0,1)$
$\text{C.}$ $(-\infty,-1) \cup(1,+\infty)$
$\text{D.}$ $(-1,0) \cup(0,1)$
若直线 $\frac{x}{a}+\frac{y}{b}=1$ 与圆 $x^{2}+y^{2}=1$ 有公共点, 则（ ）
$\text{A.}$ $a^{2}+b^{2} \leqslant 1$
$\text{B.}$ $a^{2}+b^{2} \geqslant 1$
$\text{C.}$ $\frac{1}{a^{2}}+\frac{1}{b^{2}} \leqslant 1$
$\text{D.}$ $\frac{1}{a^{2}}+\frac{1}{b^{2}} \geqslant 1$
已知三棱柱 $\mathrm{ABC}-\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ 的侧棱与底面边长都相等, $\mathrm{A}_{1}$ 在底面 $\mathrm{ABC}$ 内的射影为 $\triangle A B C$ 的中心, 则 $A B_{1}$ 与底面 $A B C$ 所成角的正弦值等于（ ）
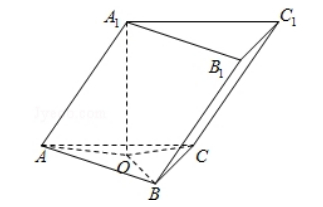
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{\sqrt{2}}{3}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\frac{2}{3}$
12. (5 分) 如图,一环形花坛分成 $A, B, C, D$ 四块, 现有 4 种不同的花供选 种, 要求在每块里种 1 种花, 且相邻的 2 块种不同的花, 则不同的种法总数 为 ( )
$\text{A.}$ 96
$\text{B.}$ 84
$\text{C.}$ 60
$\text{D.}$ 48
填空题 （共 4 题 ），请把答案直接填写在答题纸上
若 $x, y$ 满足约束条件 $x+y \geqslant 0$ $x-y+3 \geqslant 0, \quad$ 则 $z=2 x-y$ 的最大值为 （ ）
已知抛物线 $\mathrm{y}=\mathrm{ax}^{2}-1$ 的焦点是坐标原点, 则以抛物线与两坐标轴的 三个交点为顶点的三角形面积为 （ ）
在 $\triangle A B C$ 中, $A B=B C, \cos B=-\frac{7}{18}$. 若以 $A, B$ 为焦点的椭圆经过点 $C$ , 则该椭圆的离心率 （ ）
等边三角形 $A B C$ 与正方形 $A B D E$ 有一公共边 $A B$, 二面角 $C-A B-D$ 的余弦值为 $\frac{\sqrt{3}}{3}, \mathrm{M}, \mathrm{N}$ 分别是 $\mathrm{AC}, \mathrm{BC}$ 的中点, 则 $\mathrm{EM}, \mathrm{AN}$ 所成角的余弦值 等于 （ ）
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
设 $\triangle A B C$ 的内角 $A, B, C$ 所对的边长分别为 $a, b, c$, 且 $a \cos B-b \cos A=$ $\frac{3}{5} c .$
(I) 求 $\frac{\tan A}{\tan B}$ 的值;
(II) 求 $\tan (\mathrm{A}-\mathrm{B}$ ) 的最大值.
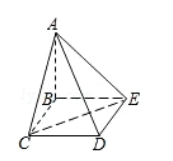
四棱雉 $A-B C D E$ 中, 底面 $B C D E$ 为矩形, 侧面 $A B C \perp$ 底面 $B C D E, B C=2$
, $C D=\sqrt{2}, \quad A B=A C$.
( I ) 证明: $\mathrm{AD} \perp \mathrm{CE}$;
（II) 设 $\mathrm{CE}$ 与平面 $\mathrm{ABE}$ 所成的角为 $45^{\circ}$, 求二面角 $C-A D-E$ 的大小.
已知函数 $\mathrm{f}(\mathrm{x})=-\mathrm{x}^{2}+a \mathrm{x}+1-\ln \mathrm{x}$.
(I) 当 $a=3$ 时，求函数 $f(x)$ 的单调递增区间;
(II ) 若 $\mathrm{f}(\mathrm{x})$ 在区间 $\left(0, \frac{1}{2}\right)$ 上是减函数, 求实数 $\mathrm{a}$ 的取值范围.
已知 5 只动物中有 1 只患有某种疾病, 需要通过化验血液来确定 患病的动物. 血液化验结果呈阳性的即为患病动物, 呈阴性即没患病. 下面 是两种化验方法:
方案甲: 逐个化验, 直到能确定患病动物为止.
方案乙: 先任取 3 只, 将它们的血液混在一起化验. 若结果呈阳性则表明患病动 物为这 3 只中的 1 只, 然后再逐个化验, 直到能确定患病动物为止; 若结果 呈阴性则在另外 2 只中任取 1 只化验.
( I ) 求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(III) $\xi$ 表示依方案乙所需化验次数, 求 $\xi$ 的期望.
双曲线的中心为原点 $\mathrm{O}$, 焦点在 $\mathrm{x}$ 轴上, 两条渐近线分别为 $\mathrm{I}_{1}, \mathrm{I}_{2}$, 经过右焦点 $F$ 垂直于 $I_{1}$ 的直线分别交 $l_{1}, I_{2}$ 于 $A, B$ 两点. 已知 $|\overrightarrow{O A}| 、|\overrightarrow{A B}|$ 、
$|\overrightarrow{\mathrm{OB}}|$ 成等差数列, 且 $\overrightarrow{\mathrm{BF}}$ 与 $\overrightarrow{\mathrm{FA}}$ 同向.
（I）求双曲线的离心率;
（II ) 设 $A B$ 被双曲线所截得的线段的长为 4 , 求双曲线的方程.
设函数 $f(x)=x-x \ln x$. 数列 $\left\{a_{n}\right\}$ 满足 $0 < a_{1} < 1, a_{n+1}=f\left(a_{n}\right)$.
（I） 证明：函数 $f(x)$ 在区间 $(0,1 ）$ 是增函数;
(II ) 证明: $a_{n} < a_{n+1} < 1$;
（III）设 $b \in\left(a_{1}, 1\right)$, 整数 $k \geqslant \frac{a_{1}-b}{a_{1} \ln b}$. 证明: $a_{k+1}>b$.