解答题 (共 17 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图, 在菱形 $A B C D$ 中, $A B=12, \angle A=60^{\circ}$, 点 $E$ 为边 $A D$ 的中点, $F$ 为射线 $A B$ 上一动点, 连接 $E F$, 把 $\triangle A E F$ 沿 $E F$ 折叠, 得到 $\triangle A^{\prime} E F$, 当 $A^{\prime} F$ 与菱形的边垂直时, 线段 $A F$的长为
如图, 菱形 $A B C D$ 的边长 $A B=16, \angle D=60^{\circ}, M$ 是 $C D$ 边上一点, $D M=6, N$ 是 $A B$ 边上一动点, 将梯形 $C M N B$ 沿直线 $M N$ 折叠, $C$ 对应点 $C^{\prime}$. 当 $A C^{\prime}$ 的长度最小时, $A N$ 的长为

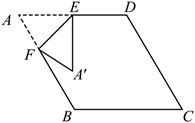
如图, 在四边形纸片 $A B C D$ 中, $A D \| B C, A B=10, \angle B=60^{\circ}$, 将纸片折叠, 使点 $B$ 落在 $A D$边上的点 $G$ 处, 折痕为 $E F$, 若 $\angle B F E=45^{\circ}$, 则 $B F$ 的长为
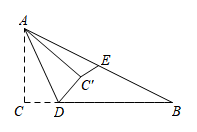
如图, 在Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, A C=6, B C=8$, 点 $F$ 在边 $A C$ 上, 并且 $C F=2$, 点 $E$ 为边 $B C$上的动点, 将 $\triangle C E F$ 沿直线 $E F$ 翻折, 点 $C$ 落在点 $P$ 处, 则点 $P$ 到边 $A B$ 距离的最小值是 $\qquad$ .

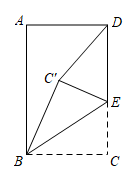
如图, 在矩形 $A B C D$ 中, $A B=8, A D=5$, 点 $E$ 是线段 $C D$ 上的一点 (不与点 $D, C$ 重合), 将 $\triangle B C E$沿 $B E$ 折叠, 使得点 $C$ 落在 $C^{\prime}$ 处, 当 $\triangle C^{\prime} C D$ 为等腰三角形时, $C E$ 的长为 $\qquad$ .
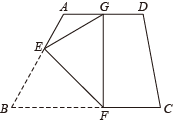
如图, 在矩形 $A B C D$ 中, $C D=3$, 对角线 $A C=5$, 点 $G, H$ 分别是线段 $A D, A C$ 上的点, 将 $\triangle A C D$沿直线 $G H$ 折叠, 点 $C, D$ 分别落在点 $E, F$ 处. 当点 $E$ 落在折线 $C A D$ 上, 且 $A E=1$ 时, $C H$ 的长为
在数学探究活动中, 小美将矩形 $A B C D$ 纸片先对折, 展开后折痕是 $E F$, 点 $M$ 为 $B C$ 边上一动点, 连接 $A M$, 过点 $M$ 作 $M N \perp A M$ 交 $C D$ 于点 $N$. 将 $\triangle M C N$ 沿 $M N$ 翻折, 点 $C$ 恰好落在线段 $E F$ 上, 已知矩形 $A B C D$ 中 $A B=4, B C=6$, 那么 $B M$ 的长为
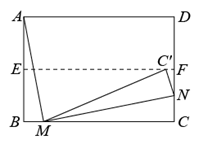
如图, 矩形 $A B C D$ 中, $A B=4, A D=6$, 点 $E$ 为 $A D$ 中点, 点 $P$ 为线段 $A B$ 上一个动点, 连接 $E P$, 将 $\triangle A P E$ 沿 $P E$ 折叠得到 $\triangle F P E$, 连接 $C E, D F$, 当线段 $D F$ 被 $C E$ 垂直平分时, $A F$ 则线的长为
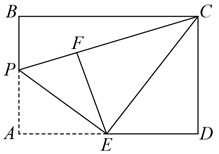
如图, 在矩形 $A B C D$ 中, $A B=2, A D=1, E$ 是 $A B$ 上一个动点, $F$ 是 $A D$ 上一个动点 (点 $F$不与点 $D$ 重合), 连接 $E F$, 把 $\triangle A E F$ 沿 $E F$ 折叠, 使点 $A$ 的对应点 $A^{\prime}$ 总落在 $D C$ 边上. 若 $\triangle A^{\prime} E C$是以 $A^{\prime} E$ 为腰的等腰三角形, 则 $A^{\prime} D$ 的长为
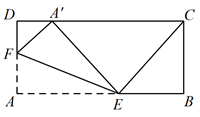
如图, 长方形 $A B C D$ 中, $A D=3, A B=5$, 点 $E$ 为射线 $C D$ 上一动点(不与 $D$ 重合), 将 $\triangle A D E$沿 $A E$ 折叠得到 $\triangle D^{\prime} A E$, 连接 $D^{\prime} B$, 若 $\triangle A B D^{\prime}$ 为直角三角形, 则 $A E=$
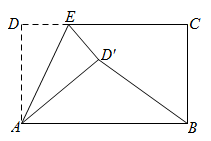
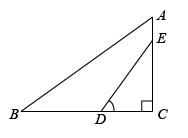
如图, 已知 $Rt \triangle A B C$ 中, $\angle B=90^{\circ}, \angle A=60^{\circ}, A C=10$, 点 $M 、 N$ 分别在线段 $A C 、 A B$ 上,将 $\triangle A N M$ 沿直线 $M N$ 折叠, 使点 $A$ 的对应点 $D$ 恰好落在线段 $B C$ 上, 当 $\triangle D C M$ 为直角三角形时,折痕 $M N$ 的长为
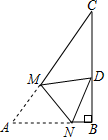
如图, 在 $Rt \triangle A B C$ 中, $\angle C=90^{\circ}, A C=12, B C=16$, 点 $D 、 E$ 分别是边 $B C 、 A C$ 上的点, 且 $\angle E D C=\angle A$, 将 $\triangle A B C$ 沿 $D E$ 对折, 若点 $C$ 恰好落到了 $\triangle A B C$ 的外部, 则折痕 $D E$ 的长度范围是
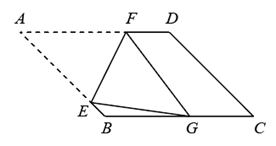
如图, 在 $\square A B C D$ 中, 点 $E, F$ 分别在边 $A B 、 A D$ 上, 将 $\triangle A E F$ 沿 $E F$ 折叠, 点 $A$ 恰好落在 $B C$边上的点 $G$ 处. 若 $\angle A=45^{\circ}, A B=6 \sqrt{2}, 5 B E=A E$. 则 $A F$ 长度为
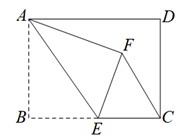
|如图, 矩形 $A B C D$ 中, $A B=6, B C=8, E$ 是 $B C$ 边上的一个动点, 将 $\triangle A B E$ 沿 $A E$ 折叠, 得到 $\triangle A F E$, 则当 $C F$ 最小时, 折痕 $A E$ 长为
如图, 在正方形 $A B C D$ 中, $A B=8, E$ 是 $C D$ 上一点, 且 $D E=2, F$ 是 $A D$ 上一动点, 连接 $E F$, 若将 $\triangle D E F$ 沿 $E F$ 翻折后, 点 $D$ 落在点 $D^{\prime}$ 处, 则点 $D^{\prime}$ 到点 $B$ 的最短距离为 $\qquad$ .
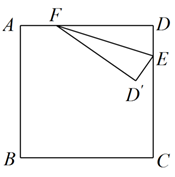
如图, 已知在矩形纸片 $A B C D$ 中, $A B=2, B C=2 \sqrt{2}$, 点 $E$ 是 $A B$ 的中点, 点 $F$ 是 $A D$ 边上的一个动点, 将 $\triangle A E F$ 沿 $E F$ 所在直线翻折, 得到 $\triangle A^{\prime} E F$, 连接 $A^{\prime} C, A^{\prime} D$, 则当 $\triangle A^{\prime} D C$ 是以 $A^{\prime} D$为腰的等腰三角形时, $A F$ 的长是
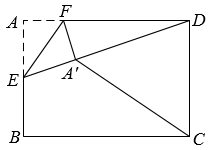
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=2, B C=4, E$ 为边 $A B$ 的中点, 点 $D$ 是 $B C$ 边上的动点, 把 $\triangle A C D$ 沿 $A D$ 翻折, 点 $C$ 落在 $C^{\prime}$ 处, 若 $\triangle A C^{\prime} E$ 是直角三角形, 则 $C D$ 的长为 $\qquad$