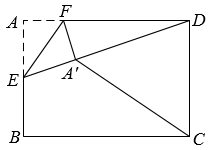
如图, 已知在矩形纸片 $A B C D$ 中, $A B=2, B C=2 \sqrt{2}$, 点 $E$ 是 $A B$ 的中点, 点 $F$ 是 $A D$ 边上的一个动点, 将 $\triangle A E F$ 沿 $E F$ 所在直线翻折, 得到 $\triangle A^{\prime} E F$, 连接 $A^{\prime} C, A^{\prime} D$, 则当 $\triangle A^{\prime} D C$ 是以 $A^{\prime} D$为腰的等腰三角形时, $A F$ 的长是