单选题 (共 8 题 ),每题只有一个选项正确
当 $x \rightarrow 0$ 时, 若 $x-\tan x$ 与 $x^k$ 是同阶无穷小, 则 $k=(\quad)$
$\text{A.}$ 1 .
$\text{B.}$ 2 .
$\text{C.}$ 3 .
$\text{D.}$ 4 .
设函数 $f(x)=\left\{\begin{array}{ll}x|x|, & x \leqslant 0, \\ x \ln x, & x>0,\end{array}\right.$ 则 $x=0$ 是 $f(x)$ 的 $\quad$ )
$\text{A.}$ 可导点, 极值点.
$\text{B.}$ 不可导点, 极值点.
$\text{C.}$ 可导点,非极值点.
$\text{D.}$ 不可导点, 非极值点.
设 $\left\{u_n\right\}$ 是单调增加的有界数列,则下列级数中收敛的是()
$\text{A.}$ $\sum_{n=1}^{\infty} \frac{u_n}{n}$.
$\text{B.}$ $\sum_{n=1}^{\infty}(-1)^n \frac{1}{u_n}$.
$\text{C.}$ $\sum_{n=1}^{\infty}\left(1-\frac{u_n}{u_{n+1}}\right)$.
$\text{D.}$ $\sum_{n=1}^{\infty}\left(u_{n+1}^2-u_n^2\right)$.
设函数 $Q(x, y)=\frac{x}{y^2}$. 如果对上半平面 $(y>0)$ 内的任意有向光滑封闭曲线 $C$ 都有 $\oint_C P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=0$, 那么函数 $P(x, y)$ 可取为 $(\quad)$
$\text{A.}$ $y-\frac{x^2}{y^3}$.
$\text{B.}$ $\frac{1}{y}-\frac{x^2}{y^3}$.
$\text{C.}$ $\frac{1}{x}-\frac{1}{y}$.
$\text{D.}$ $x-\frac{1}{y}$.
设 $\boldsymbol{A}$ 是 3 阶实对称矩阵, $\boldsymbol{E}$ 是 3 阶单位矩阵。若 $\boldsymbol{A}^2+\boldsymbol{A}=2 \boldsymbol{E}$ ,且 $|\boldsymbol{A}|=4$ ,则二次型 $\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$ 的规范形为()
$\text{A.}$ $y_1^2+y_2^2+y_3^2$.
$\text{B.}$ $y_1^2+y_2^2-y_3^2$.
$\text{C.}$ $y_1^2-y_2^2-y_3^2$.
$\text{D.}$ $-y_1^2-y_2^2-y_3^2$.
如图所示, 有 3 张平面两两相交, 交线相互平行, 它们的方程$a_{i 1} x+a_{i 2} y+a_{i 3} z=d_i(i=1,2,3)$ 组成的线性方程组的系数矩阵和增广矩阵分别记为 $\boldsymbol{A}, \overline{\boldsymbol{A}}$, 则
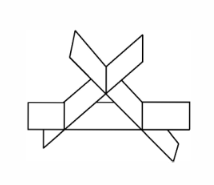
$\text{A.}$ $r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=3$.
$\text{B.}$ $r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=2$.
$\text{C.}$ $r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=2$.
$\text{D.}$ $r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=1$.
设 $A, B$ 为随机事件,则 $P(A)=P(B)$ 的充分必要条件是()
$\text{A.}$ $P(A \cup B)=P(A)+P(B)$.
$\text{B.}$ $P(A B)=P(A) P(B)$.
$\text{C.}$ $P(A \bar{B})=P(B \bar{A})$.
$\text{D.}$ $P(A B)=P(\bar{A} \bar{B})$.
设随机变量 $X$ 与 $Y$ 相互独立,且都服从正态分布 $N\left(\mu, \sigma^2\right)$ ,则 $P\{|X-Y| < 1\}(\quad)$
$\text{A.}$ 与 $\mu$ 无关,而与 $\sigma^2$ 有关.
$\text{B.}$ 与 $\mu$ 有关,而与 $\sigma^2$ 无关.
$\text{C.}$ 与 $\mu, \sigma^2$ 都有关.
$\text{D.}$ 与 $\mu, \sigma^2$ 都无关.
填空题 (共 6 题 ),请把答案直接填写在答题纸上
设函数 $f(u)$ 可导, $z=f(\sin y-\sin x)+x y$, 则 $\frac{1}{\cos x} \cdot \frac{\partial z}{\partial x}+\frac{1}{\cos y} \cdot \frac{\partial z}{\partial y}=$ $\qquad$ .
微分方程 $2 y y^{\prime}-y^2-2=0$ 满足条件 $y(0)=1$ 的特解 $y=$ $\qquad$ .
幂级数 $\sum_{n=0}^{\infty} \frac{(-1)^n}{(2 n)!} x^n$ 在 $(0,+\infty)$ 内的和函数 $S(x)=$ $\qquad$ .
设 $\Sigma$ 设为曲面 $x^2+y^2+4 z^2=4(z \geqslant 0)$ 的上侧, 则 $\iint_{\Sigma} \sqrt{4-x^2-4 z^2} \mathrm{~d} x \mathrm{~d} y=$ $\qquad$ .
设 $\boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)$ 为 3 阶矩阵。若 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2$ 线性无关,且 $\boldsymbol{\alpha}_3=-\boldsymbol{\alpha}_1+2 \boldsymbol{\alpha}_2$ ,则线性方程组 $\boldsymbol{A x}=\mathbf{0}$ 的通解为 $\qquad$ .
设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{l}\frac{x}{2}, 0 < x < 2,\\ 0, \text { 其他, }\end{array}\right.$ $ F(x)$ 为$X$ 的分布函数, $E(X)$为$X$的数学期望, 则 $P\{F(X)>E(X)-1\}=$ $\qquad$ .
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设函数 $y(x)$ 是微分方程 $y^{\prime}+x y=e^{-\frac{x^2}{2}}$ 满足条件 $y(0)=0$ 的特解.
(1) 求 $y(x)$ ;
(2) 求曲线 $y=y(x)$ 的凹凸区间及拐点.
设 $a, b$ 为实数,函数 $z=2+a x^2+b y^2$ 在点 $(3,4)$ 处的方向导数中,沿方向 $l=-3 i-4 j$ 的方向导数晨大研暴交值为 10 .
(1) 求 $a, b$ ;
(2) 求曲面 $z=2+a x^2+b y^2(z \geq 0)$ 的面积.
求曲线 $y=e^{-x} \sin x(x \geq 0)$ 与 $x$ 轴所围图形的面积.
设 $a_n=\int_0^1 x^n \sqrt{1-x^2} \mathrm{~d} x(n=1,2,3, \cdots)$.
(1) 证明: 数列 $\left\{a_n\right\}$ 单调递减,且
$$
a_n=\frac{n-1}{n+2} a_{n-2}(n=2,3, \cdots) ;
$$
(2) 求极限 $\lim _{n \rightarrow \infty} \frac{a_n}{a_{n-1}}$.
设 $\Omega$ 是由锥面 $x^2+(y-z)^2=(1-z)^2(0 \leq z \leq 1)$与平面 $z=0$ 所围成的锥体,求 $\Omega$ 的形心坐标.
设向量组
$$
\alpha_1=(1,2,1)^T, \alpha_2=(1,3,2)^T, \alpha_3=(1, a, 3)^T
$$
为 $R^3$ 的一组基,
$\beta=(1,1,1)^T$ 在这个基下的坐标为 $(b, c, 1)$.
(1) 求 $a, b, c$ 的值;
(2) 证明 $\alpha_2, \alpha_3, \beta$ 为 $R^3$ 的一组基,并求 $\alpha_2, \alpha_3, \beta$ 到 $\alpha_1, \alpha_2, \alpha_3$ 的过渡矩阵。
已知矩阵 $A=\left(\begin{array}{ccc}-2 & -2 & 1 \\ 2 & x & -2 \\ 0 & 0 & -2\end{array}\right)$ 与 $B=\left(\begin{array}{ccc}2 & 1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & y\end{array}\right)$ 相似.
(1)求 $x, y$ ;
(2) 求可逆矩阵 $P$ ,使得 $P^{-1} A P=B$.
设随机变量 $X$ 与 $Y$ 相互独立, $X$ 服从参数为 1 的指数分布, $Y$ 的概率分布为
$$
P\{Y=-1\}=p, P\{Y=1\}=1-p(0 < p < 1) .
$$
令 $Z=X Y$ ,
(1) 求 $Z$ 的概率密度;
(2) $p$ 为何值时, $X$ 与 $Z$ 不相关;
(3) $X$ 与 $Z$ 是否相互独立.
设总体 $X$ 的概率密度为
$$
f\left(x, \sigma^2\right)= \begin{cases}\frac{A}{\sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} & , x \geq \mu, \\ 0, & x < \mu\end{cases}
$$
其中 $\mu$ 是已知参数, $\sigma>0$ 是未知参数, $A$ 是常数, $X_1, X_2, \cdots, X_n$ 是来自总体 $X$ 的简单随机样本.
(1) 求 $\boldsymbol{A}$ ;
(2) 求 $\sigma^2$ 的最大似然估计量.