一、单选题 (共 8 题 ),每题只有一个选项正确
1. 已知集合 , 则 .
2. 若复数 满足 , 则 的虚部为
3. 多项选择题是新高考数学试卷中增加的新题型, 四个选项 中至少有两个选项正确, 并规定: 如果选择错误了选项就不得分. 若某题的正确答案是 , 某考生随机选择了 2 个选项, 则其能得分的概率是
4. 蹴鞠 (如图所示), 又名蹴球, 蹴圆, 筑球, 踢圆等, 蹴有用脚蹴、踢、蹋, 鞠最早系外包皮革、内实米的球, 因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球. 2006 年 5 月 20 日, 蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录, 已知某鞠的表面上有四个点
、
、、 满足
, 则该的表面积为

5. 已知四边形 满足 , 点 满足 , 若 , 则 .
3
2
6. 已知双曲线 的左右焦点分别为 为坐标原点, 过 作 的一条渐近线的垂线,垂足为 , 且 , 则 的离心率为
2
5
7. 已知数列 中, , 若 , 则下列结论中正确的是
8. 已知实数 满足 , 则满足条件的 的最小正整数为
1
3
5
7
二、多选题 (共 3 题 ),每题有多个选项正确
9. 已知由样本数据点集合 (其中 ) 求得的回归直线方程 , 记此模型对应的相关指数为 . 观察残差图发现: 除了数据点 和 明显偏离横轴, 其余各点均密集均匀分布, 剔除这两个数据点后重新求得的回归直线方程 , 记此模型对应的相关指数为 . 则下列结论中正确的是
变量 与 正相关
记 , 则
10. 设 是抛物线 的焦点, 直线 与抛物线 交于 两点, 为坐标原点, 则下列结论正确的是
可能大于 0
若点 , 则
若在抛物线上存在唯一一点 (异于 ), 使得 , 则
11. 如图, 已知圆柱母线长为 4 , 底面圆半径为
, 梯形
内接于下底面圆,
是直径,
, 过点
向上底面作垂线, 垂足分别为
, 点
,
分别是线段
上的动点, 点
为上底面圆内 (含边界) 任意一点, 则
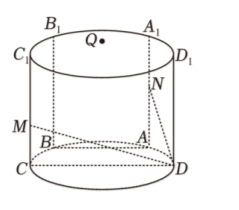
若平面 交线段 于点 , 则
若平面 过点 , 则直线 过定点
的周长为定值
当点 在上底面圆周上运动时, 记直线 与下底面所成角分别为 , 则 的取值范围是 ,
三、填空题 (共 8 题 ),请把答案直接填写在答题纸上
12. 已知函数 有三个零点, 求 的取值范围
13. 设 的内角 所对边的长分别是 , 且 为 边上的中点, 且 , 则
14. 若数集 的子集满足: 至少含有 2 个元素, 且任意两个元素之差的绝对值大于 1 , 则称该子集为数集 的超子集. 已知集合, 记 , 记 的超子集的个数为 , 当 的超子集个数为 221 个时,
15. 智能体温计由于测温方便、快捷, 已经逐渐代替水银体温计应用于日常体温检测. 调查发现,使用水银体温计测温结果与人体的真实体温基本一致, 而使用智能体温计测量体温可能会产生误差. 对同一人而言, 如果用智能体温计与水银体温计测温结果相同, 我们认为智能体温计“测温准确”; 否则, 我们认为智能体温计“测温失误”. 现在某社区随机抽取了 20 人用两种体温计进行体温检测, 数据如表. 用频率估计概率, 解答下列问题:
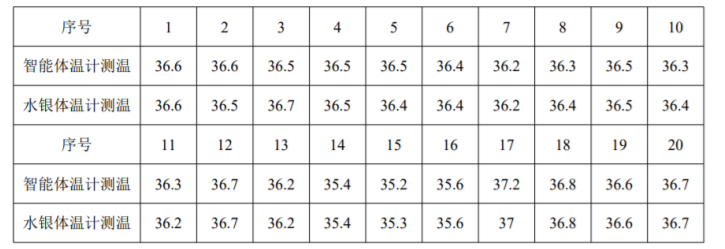
(1) 从该社区中任意抽查 3 人用智能体温计测量体温, 设随机变量
为使用智能体温计“测温准确”的人数, 求
的分布列与数学期望值;
(2) 医学上通常认为, 人的体温不低于
且不高于
时处于“低热”状态. 该社区某一天用智能体温计测温的结果显示, 有 3 人的体温都是
, 能否由上表中的数据来认定这 3 个人中至少有 1 人处于“低热”状态? 说明理由.
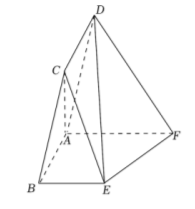
16. 四边形
是平行四边形,
, 四边形
是梯形,
, 且
,
, 平面
平面
.
(1) 求证:
;
(2) 求直线
与平面
所成角的正弦值.
17. 设点 为抛物线 的焦点, 过点 且斜率为 的直线与 交于 两点 ( 为坐标原点).
(1)求抛物线 的方程;
(2)过点 作两条斜率分别为 的直线 , 它们分别与抛物线 交于点 和 . 已知 , 问: 是否存在实数 , 使得 为定值?若存在, 求 的值, 若不存在, 请说明理由.
18. 设数列 的前 项和为 , 且满足 .
(1)求数列 的通项公式;
(2)解关于 的不等式: ;
(3)若 , 求证:数列 前 项和小于 .
19. 已知函数 .
(1)若曲线 在 处的切线过原点, 求 的值;
(2)当 时, , 求 的取值范围.