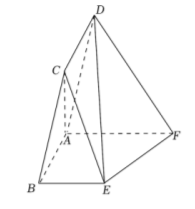
四边形 $\mathrm{ABCD}$ 是平行四边形, $\angle \mathrm{CBA}=\frac{\pi}{4}$, 四边形 $\mathrm{ABEF}$ 是梯形, $\mathrm{BE} / / \mathrm{AF}$, 且 $\mathrm{AB} \perp \mathrm{AF}$, $\mathrm{AB}=\mathrm{BE}=\frac{1}{2} \mathrm{AF}=1, \mathrm{BC}=\sqrt{2}$, 平面 $\mathrm{ABCD} \perp$ 平面 $\mathrm{ABEF}$.
(1) 求证: $\mathrm{AC} \perp \mathrm{EF}$;
(2) 求直线 $\mathrm{EC}$ 与平面 $\mathrm{EFD}$ 所成角的正弦值.
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$