单选题 (共 8 题 ),每题只有一个选项正确
已知复数 $z$ 满足 $z+z \mathrm{i}=\mathrm{i}$, 则 $z=$
$\text{A.}$ $\frac{1}{2}+\frac{1}{2} \mathrm{i}$
$\text{B.}$ $\frac{1}{2}-\frac{1}{2} \mathrm{i}$
$\text{C.}$ $1+\mathrm{i}$
$\text{D.}$ $1-\mathrm{i}$
已知集合 $A=\left\{x \in \mathbf{R} \mid x^2-2 x-3>0\right\}$, 集合 $B$ 满足 $B \varsubsetneqq A$, 则 $B$ 可以为
$\text{A.}$ $[-1,3]$
$\text{B.}$ $(-\infty,-1]$
$\text{C.}$ $(-\infty,-1)$
$\text{D.}$ $(-\infty, 3)$
校举行“云翔杯”学生篮球比赛, 统计部分班级的得分数据如下:

$\text{A.}$ 得分的中位数为 28
$\text{B.}$ 得分的极差为 8
$\text{C.}$ 得分的众数为 34
$\text{D.}$ 得分的平均数为 31
已知 $m, n$ 是不同的直线, $\alpha, \beta$ 是不同的平面, 则
$\text{A.}$ 若 $\alpha / / \beta, m / / \alpha, n / / \beta$, 则 $m / / n$
$\text{B.}$ 若 $\alpha / / \beta, m \perp \alpha, n / / \beta$, 则 $m / / n$
$\text{C.}$ 若 $\alpha \perp \beta, m \perp \alpha, n \perp \beta$, 则 $m \perp n$
$\text{D.}$ 若 $\alpha \perp \beta, m / / \alpha, n / / \beta$, 则 $m \perp n$
在 $\triangle A B C$ 中, 若 $A C^2+B C^2=5 A B^2$, 则 $\frac{\tan C}{\tan A}+\frac{\tan C}{\tan B}=$
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{2}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
已知 $\left\{a_n\right\}$ 是各项均为正数的等比数列, $a_1+a_2+a_3+a_4+a_5+a_6=10, a_1 a_2 a_3 a_4 a_5 a_6=8$, 则 $\frac{1}{a_1}+\frac{1}{a_2}+$ $\frac{1}{a_3}+\frac{1}{a_4}+\frac{1}{a_5}+\frac{1}{a_6}=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
过抛物线 $C: y^2=4 x$ 的焦点 $F$ 作直线 $l_1, l_2$, 其中 $l_1$ 与 $C$ 交于 $M, N$ 两点, $l_2$ 与 $C$ 交于 $P, Q$ 两点, 则 $\frac{1}{|F M|}+\frac{1}{|F N|}+\frac{1}{|F P|}+\frac{1}{|F Q|}=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若 $\forall x \in \mathbf{R}, x^2 \geqslant-\frac{1}{2} \cos 2 \omega x+\frac{1}{2}$, 则实数 $\omega$ 的最大值为
$\text{A.}$ 1
$\text{B.}$ 0
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{\pi}{2}$
多选题 (共 3 题 ),每题有多个选项正确
已知双曲线 $E: \frac{x^2}{a^2}-y^2=1(a>0)$ 过点 $P(4, \sqrt{3})$, 则
$\text{A.}$ 双曲线 $E$ 的实轴长为 4
$\text{B.}$ 双曲线 $E$ 的离心率为 $\frac{\sqrt{5}}{2}$
$\text{C.}$ 双曲线 $E$ 的渐近线方程为 $y= \pm 2 x$
$\text{D.}$ 过点 $P$ 且与双曲线 $E$ 仅有 1 个公共点的直线恰有 1 条
张同学从学校回家要经过 2 个路口, 假设每个路口等可能遇到红灯或绿灯, 每个路口遇到红绿灯相互独立, 记事件 A: “第 1 个路口遇到绿奵”, 事件 $B$ : “第 2 个路口遇到绿灯”, 则
$\text{A.}$ $P(A)=\frac{1}{2}$
$\text{B.}$ $P(A B)=\frac{1}{4}$
$\text{C.}$ $P(B \mid \bar{A})=\frac{1}{4}$
$\text{D.}$ $P(A+B)=\frac{3}{4}$
已知 $f(x)$ 是定义在 $\mathbf{R}$ 上的函数, 且任意 $x, y \in \mathbf{R}$, 有 $f(x+y)=f(x)+f(y), f(1)=\frac{1}{2}$, 则
$\text{A.}$ $f(x)$ 为 $\mathbf{R}$ 上的单调递增函数
$\text{B.}$ $f(x)$ 为奇函数
$\text{C.}$ 函数 $g(x)=\frac{f(x)}{\mathrm{e}^x}$ 在 $x=0$ 处取极小值
$\text{D.}$ 函数 $h(x)=f(x)-2 \sin x-1$ 只有一个非负零点
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知向量 $\boldsymbol{a}=(k, 2), \boldsymbol{b}=(2,1)$, 若 $\boldsymbol{a} \perp \boldsymbol{b}$, 则实数 $k=$
已知三棱锥 $A-B C D$ 的四个顶点都在球 $O$ 的球面上, 且 $A B=C D=\sqrt{5}, A C=B D=\sqrt{10}, A D=B C=$ $\sqrt{13}$, 则球 $O$ 的半径为
已知直线 $l_1$ 与曲线 $y=a \mathrm{e}^x$ 和 $y=\ln x-\ln a$ 都相切, 倾斜角为 $\alpha$, 直线 $l_2$ 与曲线 $y=a \mathrm{e}^x$ 和 $y=\ln x-\ln a$ 都相切, 倾斜角为 $\beta$, 则 $\tan \alpha+4 \tan \beta$ 取最小时, 实数 $a$ 的值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1) 求证: $\frac{\sin 1^{\circ}}{\sin k^{\circ} \sin (k+1)^{\circ}}=\frac{\cos k^{\circ}}{\sin k^{\circ}}-\frac{\cos (k+1)^{\circ}}{\sin (k+1)^{\circ}}$;
(2) 求值: $\frac{1}{\cos 0^{\circ} \cos 1^{\circ}}+\frac{1}{\cos 1^{\circ} \cos 2^{\circ}}+\cdots+\frac{1}{\cos 44^{\circ} \cos 45^{\circ}}$.
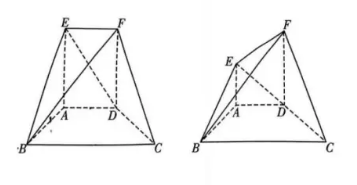
如图, $A E \perp$ 平面 $A B C D, E, F$ 在平面 $A B C D$ 的同侧, $A E / / D F, A D / / B C, A D \perp A B, A D=A B=$ $\frac{1}{2} B C=1$.
(1) 若 $B, E, F, C$ 四点在同一平面内, 求线段 $E F$ 的长;
(2)若 $D F=2 A E$, 平面 $B E F$ 与平面 $B C F$ 的夹角为 $30^{\circ}$; 求线段 $A E$ 的长.
已知函数 $f(x)=x \mathrm{e}^x$.
(1) 求 $f(x)$ 的单调区间;
(2) 若关于 $x$ 的不等式 $f(x)+f(1-x) \geqslant a$ 恒成立, 求实数 $a$ 的取值范围.
已知楠圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$, 直线 $l_1$ 与 $E$ 交于 $M(-4,0), N(-2,2)$ 两点, 点 $P$ 在线段 $M N$
上(不含端点), 过点 $P$ 的另一条直线 $l_2$ 与 $E$ 交于 $A, B$ 两点.
(1)求楠圆 $E$ 的标准方程;
(2) 若 $\overrightarrow{M P}=\overrightarrow{P N}, \overrightarrow{A P}=(7-4 \sqrt{3}) \overrightarrow{P B}$, 点 $A$ 在第二象限, 求直线 $l_2$ 的斜率;
(3) 若直线 $M A, M B$ 的斜率之和为 2 , 求直线 $l_2$ 的斜率的取值范围.
组合投资需要同时考虑风险与收益. 为了控制风险需要组合低风险资产, 为了扩大收益需要组合高收益资产. 现有两个相互独立的投资项目 $A$ 和 $B$, 单独投资 100 万元项目 $A$ 的收益记为随机变量 $X$, 单独投资 100 万元项目 $B$ 的收益记为随机变量 $Y$. 若将 100 万资金按 $\lambda A+(1-\lambda) B$ 进行组合投资, 则投资收益的随机变量 $Z$ 满足 $Z=\lambda X+(1-\lambda) Y$, 其中 $\delta \leqslant \lambda \leqslant 1$. 假设在组合投资中, 可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
(1)若 $Y \sim B(100,0.03), \lambda=0$, 求 $Z$ 的期望与方差;
(2)已知随机变量 $X$ 满足分布列:

且随机变量 $X$ 与 $Y$ 相互独立, 即 $P\left(X=x_i, Y=y_i\right)=P\left(X=x_i\right) \cdot P\left(Y=y_i\right), Z=\lambda X+$ $(1-\lambda) Y, D(X)=\sum_{i=1}^n\left(x_i-E(X)\right)^2 \cdot p_i=E(X-E(X))^2$.
求证: $D(Z)=\lambda^2 D(X)+(1-\lambda)^2 D(Y)$;
(3)若投资项目 $X$ 是高收益资产,其每年的收益满足:有 $30 \%$ 的可能亏损当前资产的一半;有 $70 \%$ 的可能增值当前资产的一倍. 投资项目 $Y$ 是低风险资产, 满足 $Y \sim B(100,0.03)$. 试问 $\lambda=0.3$ 能否满足投资第 1 年的收益否低于 17 万, 风险不高于 500 ? 请说明理由.