单选题 (共 8 题 ),每题只有一个选项正确
某校高一年级 15 个班参加朗诵比赛的得分如下: 85 87 88 89 89 90 91 91 92 93 93 93 94 96 98 ,则这组数据的 $40 \%$ 分位数为
$\text{A.}$ 90
$\text{B.}$ 91
$\text{C.}$ 90.5
$\text{D.}$ 92
已知圆 $C: x^2+y^2-4 x-14 y+45=0$ 及点 $Q(-2,3)$, 则下列说法正确的是
$\text{A.}$ 直线 $k x-y-2 k+1=0$ 与圆 $C$ 始终有两个交点
$\text{B.}$ 若 $M$ 是圆 $C$ 上任一点, 则 $|M Q|$ 的取值范围为 $[2 \sqrt{2}, 6 \sqrt{2}]$
$\text{C.}$ 若点 $P(m, m+1)$ 在圆 $C$ 上, 则直线 $P Q$ 的斜率为 $\frac{1}{4}$
$\text{D.}$ 圆 $C$ 与 $x$ 轴相切
已知向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=1, \vec{b}=(t, 2-t), \vec{a}-\vec{b}$ 与 $a$ 垂直, 则 $|\vec{a}-\vec{b}|$ 的最小值为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ 1
$\text{D.}$ 3
高一 (1) 班有 8 名身高都不相同的同学去参加红歌合唱, 他们站成前后对齐的 2 排, 每排 4 人, 则前排的同学都比后排对应的同学矮的概率为
$\text{A.}$ $\frac{1}{384}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{3}{8}$
$\text{D.}$ $\frac{1}{16}$
已知数列 $\left\{a_n\right\} 、\left\{b_n\right\}$ 的前 $n$ 项和分别为 $A_n 、 B_n$, 记 $c_n=a_n \cdot B_n+b_n \cdot A_n-$ $a_n \cdot b_n$, 则数列 $\left\{c_n\right\}$ 的前 2021 项和为
$\text{A.}$ $A_{2021}+B_{2021}$
$\text{B.}$ $\frac{A_{2021}+B_{2021}}{2}$
$\text{C.}$ $A_{2021} \cdot B_{2021}$
$\text{D.}$ $\sqrt{A_{2021} \cdot B_{2021}}$
已知球 $O$ 的直径 $|P Q|=4, A, B, C$ 是球 $O$ 球面上的三点, $\triangle A B C$ 是等边三角形, 且 $\angle A P Q=\angle B P Q=\angle C P Q=30^{\circ}$, 则三棱椎 $P-A B C$ 的体积为
$\text{A.}$ $\frac{9 \sqrt{3}}{4}$
$\text{B.}$ $\frac{27 \sqrt{3}}{4}$
$\text{C.}$ $\frac{3 \sqrt{3}}{2}$
$\text{D.}$ $\frac{3 \sqrt{3}}{4}$
已知 $\alpha \in(0, \pi)$, 且 $3 \tan \alpha=10 \cos 2 \alpha$, 则 $\cos \alpha$ 可能为
$\text{A.}$ $-\frac{\sqrt{10}}{10}$
$\text{B.}$ $-\frac{\sqrt{5}}{5}$
$\text{C.}$ $\frac{\sqrt{10}}{10}$
$\text{D.}$ $\frac{\sqrt{5}}{5}$
已知 $f(x)$ 为奇函数, 当 $x \in[0,1]$ 时, $f(x)=1-2\left|x-\frac{1}{2}\right|$, 当 $x \in(-\infty,-1], f(x)=1-e^{-1-x}$,若羔于 $x$ 的不等式 $f(x+m)>f(x)$ 恒成立, 则实数 $m$ 的取值范围为
$\text{A.}$ $(-1,0) \cup(0,+\infty)$
$\text{B.}$ $\left(\frac{1}{2}+\ln 2,+\infty\right)$
$\text{C.}$ $\left(-\frac{1}{2}-\ln 2,-1\right) \cup\left(\frac{1}{2}+\ln 2,+\infty\right)$
$\text{D.}$ $(2,+\infty)$
多选题 (共 3 题 ),每题有多个选项正确
下列选项中的两个集合相等的有
$\text{A.}$ $P=\{x \mid x=2 n, n \in \boldsymbol{Z}\}, Q=\{x \mid x=2(n+1), n \in \boldsymbol{Z}\}$
$\text{B.}$ $P=\left\{x \mid x=2 n-1, n \in \boldsymbol{N}_{+}\right\}, Q=\left\{x \mid x=2 n+1, n \in \boldsymbol{N}_{+}\right\}$
$\text{C.}$ $P=\left\{x \mid x^2-x=0\right\}, Q=\left\{x \left\lvert\, x=\frac{1+(-1)^n}{2}\right., n \in \boldsymbol{Z}\right\}$
$\text{D.}$ $P=\{x \mid y=x+1\}, Q=\{(x, y) \mid y=x+1\}$
如图, 一个质点在半径为 2 的圆 $O$ 上以点 $P$ 为起始点, 沿逆时针方向运动, 每 $3 s$ 转一圈. 则该质点到 $x$ 轴的距离 $y$ 是关于运动时间 $t$ 的函数, 则下列说法正确的是
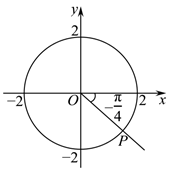
$\text{A.}$ 函数 $y$ 的最小正周期是 $\frac{3}{2}$
$\text{B.}$ 函数 $y$ 的最小正周期是 $3 \pi$
$\text{C.}$ $y=\left|2 \cos \left(\frac{2 \pi}{3} t-\frac{\pi}{4}\right)\right|$
$\text{D.}$ $y=\left|2 \sin \left(\frac{2 \pi}{3} t-\frac{\pi}{4}\right)\right|$
定义: 对于定义在区间 $I$ 上的函数 $f(x)$ 和正数 $\alpha(0 < \alpha \leq 1)$, 若存在正数 $M$, 使得不等式 $\left|f\left(x_1\right)-f\left(x_2\right)\right| \leq M\left|x_1-x_2\right|^\alpha$ 对任意 $x_1, x_2 \in I$ 恒成立, 则称函数 $f(x)$在区间 $I$ 上满足 $\alpha$ 阶李普希兹条件,则下列说法正确的有
$\text{A.}$ 函数 $f(x)=\sqrt{x}$ 在 $[1,+\infty)$ 上满足 $\frac{1}{2}$ 阶李普希兹条件
$\text{B.}$ 若函数 $f(x)=x \ln x$ 在 $[1, e]$ 上满足一阶李普希兹条件, 则 $M$ 的最小值为 $e$
$\text{C.}$ 若函数 $f(x)$ 在 $[a, b]$ 上满足 $M=k(0 < k < 1)$ 的一阶李普希兹条件, 且方程 $f(x)=x$ 在区间 $[a, b]$ 上有解 $x_0$, 则 $x_0$ 是方程 $f(x)=x$ 在区间 $[a, b]$ 上的唯一解
$\text{D.}$ 若函数 $f(x)$ 在 $[0,1]$ 上满足 $M=1$ 的一阶李普希兹条件, 且 $f(0)=f(1)$, 则对任意函数 $f(x), \forall x_1, x_2 \in[0,1]$, 恒有 $\left|f\left(x_1\right)-f\left(x_2\right)\right| \leq \frac{1}{2}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知复数 $z=(1-a)+\left(a^2-1\right) i(a>1)$, 则 $z$ 在复平面内对应的点所在的象限为象限.
已知函数 $f(x)=m x+{ }_{\ln } x, g(x)=x^2-m x$, 若曲线 $y=f(x)$ 与曲线 $y=$ $g(x)$ 存在公切线, 则实数 $m$ 的最大值为
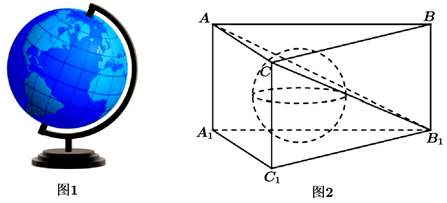
14. (本题 5 分) 地球仪是地理教学中的常用教具.如图 1 所示, 地球仪的赤道面(与转轴垂直)与黄道面(与水平面平行)存在一个夹角, 即黄赤交角, 大小约为 $23.5^{\circ}$. 为锻炼动手能力, 某同学制作了一个半径为 $4 \mathrm{~cm}$ 的地球仪(不含支架), 并将其放入坚直放置的正三棱柱 $A B C-A_1 B_1 C_1$ 中(姿态保持不变), 使地球仪与该三棱柱的三个侧面相切, 如图 2 所示.此时平面 $A B_1 C$ 恰与地球仪的赤道面平行, 则三棱柱 $A B C-A_1 B_1 C_1$ 的外接球体积为 .(参考数据: $\tan 23.5^{\circ} \approx 0.43$ )
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
为落实中央“坚持五育并举, 全面发展素质教育, 强化体育锻炼”的精神, 某高中学校鼓励学生自发组织各项体育比赛活动, 甲、乙两名同学利用课余时间进行乒乓球比赛, 规定: 每一局比赛中获胜方记 1 分, 失败方记 0 分, 没有平局, 首先获得 5 分者获胜, 比赛结束.假设每局比赛甲获胜的概率都是 $\frac{3}{5}$.
(1) 求比赛结束时恰好打了 6 局的概率;
(2) 若甲以 3: 1 的比分领先时, 记 $X$ 表示到结束比赛时还需要比赛的局数, 求 $X$ 的分布列及期望.
已知函数 $f(x)=x \ln x-a x^2+a(a \in R)$.
(1) 若函数 $f(x)$ 在 $x=1$ 处的切线与直线 $2 x-y+1=0$ 垂直, 求实数 $a$ 的值.
(2) 若函数 $f(x)$ 存在两个极值点, 求实数 $a$ 的取值范围.
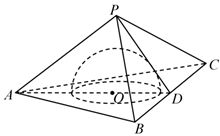
如图, 在正三棱椎 $P-A B C$ 中, 有一半径为 1 的半球, 其底面圆 $O$ 与正三棱椎的底面贴合, 正三棱椎的三个侧面都和半球相切. 设点 $D$ 为 $B C$ 的中点, $\angle A D P=\alpha$.
(1)用 $\alpha$ 分别表示线段 $B C$ 和 $P D$ 长度;
(2)当 $\alpha \in\left(0, \frac{\pi}{2}\right)$ 时, 求三棱椎的侧面积 $S$ 的最小值.
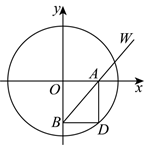
如图, $D$ 为圆 $O: x^2+y^2=1$ 上一动点, 过点 $D$ 分别作 $x$ 轴, $y$ 轴的垂线, 垂足分别为 $A, B$, 连接 $B A$ 并延长至点 $W$, 使得 $|W A|=1$, 点 $W$ 的轨迹记为曲线 $C$.
(1)求曲线 $C$ 的方程;
(2) 若过点 $K(-2,0)$ 的两条直线 $l_1, l_2$ 分别交曲线 $C$ 于 $M, N$ 两点, 且 $l_1 \perp l_2$, 求证: 直线 $M N$ 过定点;
(3)若曲线 $C$ 交 $y$ 轴正半轴于点 $S$, 直线 $x=x_0$ 与曲线 $C$ 交于不同的两点 $G, H$, 直线 $S H$, $S G$ 分别交 $x$ 轴于 $P, Q$ 两点. 请探究: $y$ 轴上是否存在点 $R$, 使得 $\angle O R P+\angle O R Q=\frac{\pi}{2}$ ?若存在, 求出点 $R$ 坐标; 若不存在, 请说明理由.
对于无穷数列 $\left\{a_n\right\}$, “若存在 $a_m-a_k=t\left(m, k \in N^*, m>k\right)$, 必有 $a_{m+1}-a_{k+1}=t$,则称数列 $\left\{a_n\right\}$ 具有 $P(t)$ 性质.
(1) 若数列 $\left\{a_n\right\}$ 满足 $a_n=\left\{\begin{array}{cc}2 n & (n=1,2) \\ 2 n-5 & \left(n \geq 3, n \in N^*\right)\end{array}\right.$, 判断数列 $\left\{a_n\right\}$ 是否具有 $P(1)$ 性质?是否具有 $P(4)$ 性质?
(2) 对于无穷数列 $\left\{a_n\right\}$, 设 $T=\left\{x \mid x=a_j-a_i, i < j\right\}$, 求证: 若数列 $\left\{a_n\right\}$ 具有 $P(0)$ 性质,则 $T$ 必为有限集;
(3) 已知 $\left\{a_n\right\}$ 是各项均为正整数的数列, 且 $\left\{a_n\right\}$ 既具有 $P(2)$ 性质, 又具有 $P(3)$ 性质,是否存在正整数 $N, k$, 使得 $a_N, a_{N+1}, a_{N+2}, \ldots, a_{N+k}, \ldots$ 成等差数列. 若存在, 请加以证明; 若不存在, 说明理由.