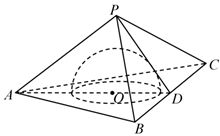
如图, 在正三棱椎 $P-A B C$ 中, 有一半径为 1 的半球, 其底面圆 $O$ 与正三棱椎的底面贴合, 正三棱椎的三个侧面都和半球相切. 设点 $D$ 为 $B C$ 的中点, $\angle A D P=\alpha$.
(1)用 $\alpha$ 分别表示线段 $B C$ 和 $P D$ 长度;
(2)当 $\alpha \in\left(0, \frac{\pi}{2}\right)$ 时, 求三棱椎的侧面积 $S$ 的最小值.
(1)用 $\alpha$ 分别表示线段 $B C$ 和 $P D$ 长度;
(2)当 $\alpha \in\left(0, \frac{\pi}{2}\right)$ 时, 求三棱椎的侧面积 $S$ 的最小值.
