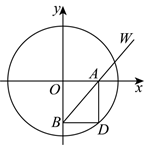
如图, $D$ 为圆 $O: x^2+y^2=1$ 上一动点, 过点 $D$ 分别作 $x$ 轴, $y$ 轴的垂线, 垂足分别为 $A, B$, 连接 $B A$ 并延长至点 $W$, 使得 $|W A|=1$, 点 $W$ 的轨迹记为曲线 $C$.
(1)求曲线 $C$ 的方程;
(2) 若过点 $K(-2,0)$ 的两条直线 $l_1, l_2$ 分别交曲线 $C$ 于 $M, N$ 两点, 且 $l_1 \perp l_2$, 求证: 直线 $M N$ 过定点;
(3)若曲线 $C$ 交 $y$ 轴正半轴于点 $S$, 直线 $x=x_0$ 与曲线 $C$ 交于不同的两点 $G, H$, 直线 $S H$, $S G$ 分别交 $x$ 轴于 $P, Q$ 两点. 请探究: $y$ 轴上是否存在点 $R$, 使得 $\angle O R P+\angle O R Q=\frac{\pi}{2}$ ?若存在, 求出点 $R$ 坐标; 若不存在, 请说明理由.
(1)求曲线 $C$ 的方程;
(2) 若过点 $K(-2,0)$ 的两条直线 $l_1, l_2$ 分别交曲线 $C$ 于 $M, N$ 两点, 且 $l_1 \perp l_2$, 求证: 直线 $M N$ 过定点;
(3)若曲线 $C$ 交 $y$ 轴正半轴于点 $S$, 直线 $x=x_0$ 与曲线 $C$ 交于不同的两点 $G, H$, 直线 $S H$, $S G$ 分别交 $x$ 轴于 $P, Q$ 两点. 请探究: $y$ 轴上是否存在点 $R$, 使得 $\angle O R P+\angle O R Q=\frac{\pi}{2}$ ?若存在, 求出点 $R$ 坐标; 若不存在, 请说明理由.
