单选题 (共 10 题 ),每题只有一个选项正确
下面四个数中最小的数是
$\text{A.}$ $-1$
$\text{B.}$ $-4 \sqrt{3}$
$\text{C.}$ 0
$\text{D.}$ $-\pi$
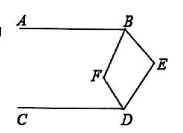
如图, 已知 $A B / / C D, \angle A B E$ 利 $\angle C D E$ 的平分线相交于 $F, \angle B E D=100^{\circ}$, 则 $\angle B F D$ 的度数为 ( )
$\text{A.}$ $100^{\circ}$
$\text{B.}$ $130^{\circ}$
$\text{C.}$ $140^{\circ}$
$\text{D.}$ $160^{\circ}$
下列计算正确的是
$\text{A.}$ $3 a \cdot a^3=a^3$
$\text{B.}$ $a+a=a^2$
$\text{C.}$ $\left(2 a^2\right)^3=6 a^6$
$\text{D.}$ $a^3 \div a=a^2$
下列计算正确的是
$\text{A.}$ $a-(-2 b+c)=a-2 b+c$
$\text{B.}$ $a^2 \cdot a^3 b=a^6 b$
$\text{C.}$ $x^3 y^4 \div y^4=x^3$
$\text{D.}$ $\left(m^3 n^2\right)^4=m^7 n^6$
在函数 $y=\frac{1}{2 x-1}$ 中, 自变量 $x$ 的取值范围是
$\text{A.}$ $x \neq \frac{1}{2}$
$\text{B.}$ $x \neq-\frac{1}{2}$
$\text{C.}$ $x>\frac{1}{2}$
$\text{D.}$ $x \geq \frac{1}{2}$
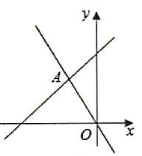
如图, 在平面直角坐标系中, 直线 $y=-2 x$ 和 $y=a x+1.2$ 相交于点 $A(m, 1)$, 则不等式 $-2 x < a x+1.2$ 的解集为
$\text{A.}$ $x < -\frac{1}{2}$
$\text{B.}$ $x < 1$
$\text{C.}$ $x>1$
$\text{D.}$ $x>-\frac{1}{2}$
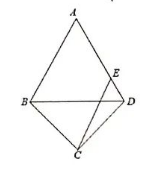
如图, $\triangle A B D$ 是等边三角形, $\triangle C B D$ 是等腰三角形, 且 $B C=D C$, 点 $E$ 是边 $A D$ 上 的一点, 满足 $C E / / A B$, 如果 $A B=8, C E=6$, 那么 $B C$ 的长是
$\text{A.}$ 6
$\text{B.}$ $2 \sqrt{7}$
$\text{C.}$ $ \sqrt{43}$
$\text{D.}$ $3 \sqrt{3}$
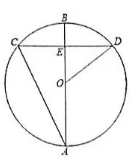
如图, $A B$ 是 $\odot O$ 的直径, 弦 $C D$ 交 $A B$ 于点 $E$, 且 $A E=C D=6, \angle B A C=\frac{1}{2} \angle B O D$, 则 $B E$ 的长为
$\text{A.}$ $\frac{5}{2}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $2$
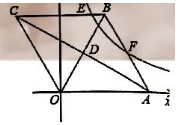
如图, 在平面直角坐标系中有菱形 $O A B C$, 点 $A$ 的坐标为 $(5,0)$, 对角线 $O B 、 A C$ 相交于 点 $D$, 双曲线 $y=\frac{k}{x}(x>0)$ 经过 $A B$ 的中点 $F$, 交 $B C$ 于点 $E$, 且 $O B \cdot A C=40$, 下列四 个结论: (1)双曲线的解析式为 $y=\frac{7}{x}(x>0)$; (2) $E$ 点的坐标是 $\left(\frac{7}{4}, 4\right)$; (3) $\sin \angle C A O=\frac{\sqrt{5}}{5}$; (4) $A C+O B=6 \sqrt{5}$. 其中正确的结论有
$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3 个
$\text{D.}$ 4 个
填空题 (共 5 题 ),请把答案直接填写在答题纸上
肥皂泡的泡壁厚度大约为 $0.0007 \mathrm{~mm}$, 用科学记数法表示 $0.0007=$
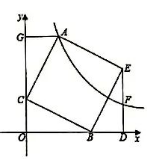
如图, 正方形 $A C B E$ 的边长是 $\sqrt{5}$, 点 $B, C$ 分别在 $x$ 轴和 $y$ 轴正半轴上, $B O=2, E D \perp x$ 轴于点 $D, E D$ 的中点 $F$ 在反比例函数 $y=\frac{k}{x}(x>0)$ 的图象上, 则 $k=$
二次函数 $y=a x^2+c$ 的图象与直线 $y=k x+b(k>0)$ 交于点 $M(-2, m), N(1, n)$ 两点 $(m n < 0)$, 则关于 $x$ 的 不等式 $a x^2+k x+(c-b)>0$ 的解集为
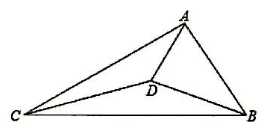
已知, 如图在 $\triangle A B C$ 中, $\angle A C B=30^{\circ}, B C=5, A C=6$, 在 $\triangle A B C$ 内部有一点 $D$, 连接 $D A 、 D B 、 D C$, 则 $D A+D B+\sqrt{2} D C$ 的最小值 是
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\sqrt{27}-\left|\sqrt{12}-4 \tan 60^{\circ}\right|+(-2)^{-2}$.
解方程: $\frac{x}{x-2}-\frac{x+1}{x+2}=\frac{x}{x^2-4}$.
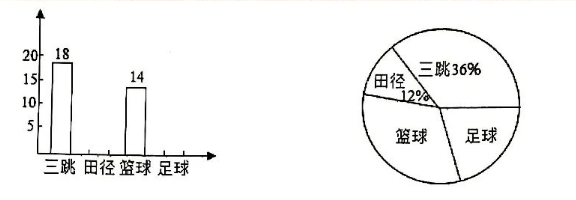
阳光中学积极开展 “阳光体育” 活动, 开设了三跳、田径、篮球和足球四种运动项目选修课. 为了解学生最崌欢 哪一种项目,从全校 3200 名学生中随机抽取了部分同学进行调查, 并绘例了如图不完整的条形统计图和扇形 统计图(部分信息末给出).
(1)请你通过计算补全条形统计图;
(2)请你求出的形统计图中 “最喜欢足球 ${ }^n$ 对应的扇形图心角度数.
(3)请你估计全校 “最喜欢篮球” 的总人数.
某服装公司在新春到来之际, 新上市 $A$ 型和 $B$ 型两款童装, 准备将 80 件 $A$ 型童装和 120 件 $B$ 型童装分配给甲、 乙两个电商平台专荬店销售 $A$ 型童装成本价 90 元, $B$ 型童装成本价 80 元, 其中 140 件给甲电商平台专卖店, 60 件给乙电商平台专卖店, 且都能卖完 两电商平台专卖店销仼这两种童装每件的价格(元)如下表:

(1) 设分配给甲电商专卖店 $A$ 型产品 $x$ 件 $(20 \leq x \leq 80$ ), 如果记这家服装公司菄出这 200 件童装的总利润为 $y$ (元), 求 $y$ 关于 $x$ 的函数关系式:
(2)如果要使得总利润最大,服装厂应当如何分配?最大利润是多少?
为了丰富学生社会实践活动, 学校组织学生到红色文化基地 $A$ 和人工智能科技馆 $C$ 参观学 习.如图, 学校在点 $B$ 处, $A$ 位于学校的东北方向, $C$ 位于学校南偏东 $30^{\circ}$ 方向, $C$ 在 $A$ 的南 侐西 $15^{\circ}$ 方向 $(30+30 \sqrt{3} \mathrm{~cm})$ 处.学生分成两组, 第一组前往 $A$ 地, 第二组前往 $C$ 地, 两组 同学同时从学校出发, 第一组乘客车, 速度是 $40 \mathrm{~km} / \mathrm{h}$, 第二组乖公交车, 速度是 $30 \mathrm{~km} / \mathrm{h}$. 哪组同学先到达目的地? 请说明理由.
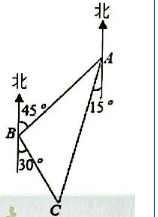
如图 1, 在 $\triangle A B C$ 中, $A B=A C, \odot \bigcirc$ 是 $\triangle A B C$ 的外接圆, 过 $C$ 作 $C D / / A B, C D$ 交 $\odot \bigcirc$ 于 $D$, 连接 $A D$ 交 $B C$ 于点 $E$, 延长 $D C$ 至点 $F$, 使 $C F=A C$, 连接 $A F$.
(1)求证: $A F$ 是 $\odot O$ 的切线;
(2)求证: $A B^2-B E^2=B E \cdot E C$;
(3) 如图 2, 若点 $G$ 是 $\triangle A C D$ 的内心, $B C \cdot B E=64$, 求 $B G$ 的长.
如图, 已知抛物线 $y=a x^2+b x+5$ 经过 $A(-5,0), B(-4,-3)$ 两点, 与 $x$ 轴的另一个交点为 $C$, 顶点为 $D$, 连接 $C D$.
(1)求该抛物线的表达式;
(2) 点 $P$ 为该抛物线上一动点 (与点 $B 、 C$ 不重合), 设点 $P$ 的横坐标为 $m$.
(1)点 $M$ 从点 $C$ 出发在线段 $C B$ 上以每秒 2 个单位长度的速度向点 $B$ 运动, 同时点 $N$ 从点 $A$ 出发以每秒 1 个单 位长度的速度向点 $C$ 运动, 当其中一个点到达终点时, 另外一个点也停止运动, 设运动时间为 $t$ 秒, 求运动时 间为多少时, $\triangle C M N$ 的面积最大, 并求出最大面积;
(2)该扐物线上是否存在点 $P$, 使得 $\angle P B C=\angle B C D$ ? 若存在, 求出所有点 $P$ 的坐标; 若不存在, 请说明理由.
