单选题 (共 8 题 ),每题只有一个选项正确
半径为 2 , 圆心角为 $112.5^{\circ}$ 的扇形的弧长为( )
$\text{A.}$ $\frac{4 \pi}{3}$
$\text{B.}$ $\frac{2 \pi}{3}$
$\text{C.}$ $\frac{5 \pi}{4}$
$\text{D.}$ $\frac{5 \pi}{8}$
在 $\triangle A B C$ 中, " $C>\frac{\pi}{3}$ " 是 " $\sin C>\frac{\sqrt{3}}{2}$ " 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
平面内三个单位向量 $\vec{a}, \vec{b}, \vec{c}$ 满足 $\vec{a}-2 \vec{b}+3 \vec{c}=\overrightarrow{0}$, 则 ( )
$\text{A.}$ $|\vec{a}+\vec{b}+\vec{c}|=3$
$\text{B.}$ $|\vec{a}+\vec{b}-\vec{c}|=3$
$\text{C.}$ $|\vec{a}-\vec{b}+\vec{c}|=3$
$\text{D.}$ $|\vec{a}-\vec{b}-\vec{c}|=3$
函数 $y=A \sin (\omega x+\varphi)(A>0, \omega>0,0 < \varphi < \pi)$ 在一个周期内的图象如图所示, 则 $\varphi=$
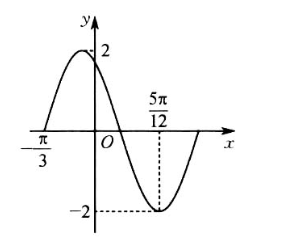
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{2 \pi}{3}$
$\text{D.}$ $\frac{5 \pi}{6}$
中国象棋中规定:马走 "日"字,象走 "田"字. 如图,在中国的半个象棋棋盘( $4 \times 8$ 的矩形中每个小步". 若马从图中的 $B$ 处跳到 $C$ 处, 且要求走的步数最少, 则马不同的行走路径有
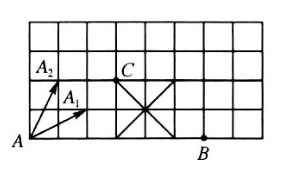
$\text{A.}$ 7 种
$\text{B.}$ 6 种
$\text{C.}$ 5 种
$\text{D.}$ 4 种
设向量 $\vec{\alpha}, \vec{\beta}$ 的夹角为 $\theta$, 定义: $\vec{\alpha} \otimes \vec{\beta}=|\vec{\alpha} \| \vec{\beta}| \sin \theta$. 若平面内互不相等的两个非零向量 $\vec{a}, \vec{b}$ 满足: $|\vec{a}|=1, \vec{a}-\vec{b}$ 与 $\vec{b}$ 的夹角为 $\frac{5 \pi}{6}$, 则 $\vec{a} \otimes \vec{b}$ 的最大值为 ( )
$\text{A.}$ 2
$\text{B.}$ $1+\frac{\sqrt{3}}{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\frac{3}{2}$
已知 $\cos 80^{\circ}=t$, 则 $\frac{3}{\sin ^2 40^{\circ}}-\frac{1}{\cos ^2 40^{\circ}}$ 的值用 $t$ 可以表示为
$\text{A.}$ $32 t$
$\text{B.}$ $24 t$
$\text{C.}$ $16 t$
$\text{D.}$ $12 t$
已知集合 $M=\{\sin \alpha, \cos \alpha, \tan \alpha\}, \alpha \in\left(0, \frac{\pi}{2}\right), N=\{a, b, a+b\}$, 则满足 $M=N$ 的集合 $N$ 的个数为
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
多选题 (共 3 题 ),每题有多个选项正确
下列函数中为奇函数的有()
$\text{A.}$ $f(x)=\cos \left(\frac{2025 \pi}{2}+2 x\right) \cos (2025 \pi+x)$
$\text{B.}$ $g(x)=\frac{\cos x}{2-\sin x}$
$\text{C.}$ $h(x)=\sqrt{1-\sin x}+\sqrt{\sin x-1}$
$\text{D.}$ $\varphi(x)=\lg \frac{\tan x+1}{\tan x-1}$
如图, 四边形 $A B C D$ 中, $A B / / C D, 2 A B=2 B C=C D, A B \perp B C, E$ 为 $C D$ 的中点, 动点 $P$ 从点 $B$ 出发, 沿 $B \rightarrow C \rightarrow E \rightarrow A$ 逆时针方向运动到点 $A$, 在此过程中, 若满足 $\overrightarrow{A P}=\lambda \overrightarrow{A B}+\mu \overrightarrow{A D}$ ( $\lambda+\mu$ 为定值) 的点 $P$ 恰有 2 个, 则 $\lambda+\mu$ 的值可能为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ 2
$\text{D.}$ 3
"奔驰定理" (若 $O$ 是 $\triangle A B C$ 内的一点, $\triangle B O C, \triangle A O C, \triangle A O B$ 的面积分别为 $S_A, S_B, S_C$, 则 $S_A$. $\overrightarrow{O A}+S_B \cdot \overrightarrow{O B}+S_C \cdot \overrightarrow{O C}=\overrightarrow{0}$ )是平面向量中一个非常优美的结论, 因为这个定理对应的图形与 "奔驰" 轿车 (Mercedes - Benz) 的标识很相似,故形象地称其为 "奔驰定理" . 若 $O$ 是锐角 $\triangle A B C$ 内的一点,则下列说法正确的有
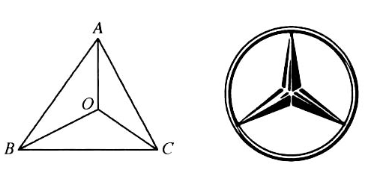
$\text{A.}$ 若 $A B=B C=C A=t$, 则 $O$ 到三边距离之和为定值 $\frac{\sqrt{3} t}{2}$
$\text{B.}$ 若 $\overrightarrow{O A}+\overrightarrow{O B}+3 \overrightarrow{O C}=\overrightarrow{0}$, 则 $\triangle O A B$ 的面积与 $\triangle A B C$ 的面积之比为 $\frac{3}{5}$
$\text{C.}$ 若 $\angle A B O=30^{\circ}, \angle A C O=60^{\circ}, \angle O B C=\angle O C B=15^{\circ}$, 则 $\tan \angle O A C=\frac{6-\sqrt{3}}{11}$
$\text{D.}$ 若 $\overrightarrow{O A} \cdot \overrightarrow{O B}=\overrightarrow{O B} \cdot \overrightarrow{O C}=\overrightarrow{O C} \cdot \overrightarrow{O A}$, 则 $\tan A \cdot \overrightarrow{O A}+\tan B \cdot \overrightarrow{O B}+\tan C \cdot \overrightarrow{O C}=\overrightarrow{0}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
在平面直角坐标系 $x O y$ 中, 角 $\alpha$ 与角 $\beta$ 均以射线 $O x$ 为始边, 它们的终边关于 $x$ 轴对称, 点 $M\left(m,-\frac{1}{2}\right)$ 在角 $\beta$ 的终边上. 若 $\sin \alpha=\frac{1}{3}$, 则 $m=$ $\qquad$ .
如图, 为了测量河对岸的塔高 $A B$, 可以选取与塔底 $B$ 在同一水平面内的两个测量基点 $C$ 与 $D$. 现测得 $\angle B C D=30^{\circ}, \angle B D C=105^{\circ}, C D=40 m$, 在点 $C$ 测得塔顶 $A$ 的仰角为 $60^{\circ}$, 则 $B D=$ $\qquad$ $m$ ,塔高 $A B=$ m.
$\qquad$

在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别为 $a, b, c, A D \perp B C$, 垂足为 $D(D$ 在边 $B C$ 上且异于端点 ), 设 $A D=h$, 且满足 $b+c=a+h$, 则 $\tan \frac{A}{2}$ 的最小值为 .
$\qquad$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\alpha$ 为锐角, $\sin \alpha-2 \cos \alpha=0$.
(1)求 $\cos ^2 \alpha-\sin \alpha \cos \alpha$ 的值;
(2) 若 $\beta \in\left(-\frac{\pi}{2}, 0\right)$, 且 $\cos (\alpha-\beta)=-\frac{\sqrt{10}}{10}$, 求 $\beta$ 的值.
如图, 在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c, B C=2 \sqrt{3}, D$ 为边 $A B$ 上的一点, 且 $a=$ $2 b \sin \left(C+\frac{\pi}{6}\right)$.
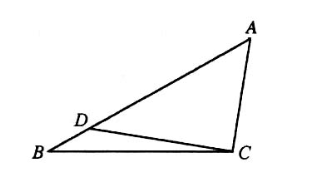
(1)求 $B$;
(2) 若 $B D=1, \angle A C D=\frac{\pi}{2}$, 求 $A C$ 的长.
如图所示, 在 $\triangle A B C$ 中, $P$ 在线段 $B C$ 上, 满足 $2 \overrightarrow{B P}=\overrightarrow{P C}, O$ 是线段 $A P$ 的中点.
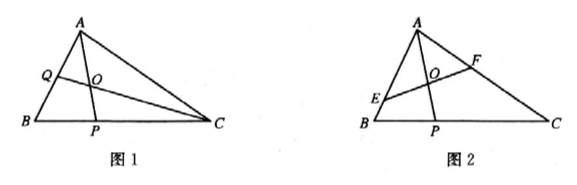
(1)延长 $C O$ 交 $A B$ 于点 $Q$ (如图1), 若4 $\overrightarrow{A B} \cdot \overrightarrow{A C}=15 \overrightarrow{A O} \cdot \overrightarrow{Q C}$, 求 $\frac{A C}{A B}$ 的值;
(2)过点 $O$ 的直线与边 $A B, A C$ 分别交于点 $E, F$ (如图2), 设 $\overrightarrow{E B}=\lambda \overrightarrow{A E}, \overrightarrow{F C}=\mu \overrightarrow{A F}$.
(i)求证: $2 \lambda+\mu$ 为定值;
(ii)设 $\triangle A E F$ 的面积为 $S_1, \triangle A B C$ 的面积为 $S_2$, 求 $\frac{S_1}{S_2}$ 的最小值.
已知函数 $f(x)=\sin \left(x+\frac{\pi}{4}\right), g(x)=-\sin 2 x+\sqrt{2} a f(x)-2$.
(1)若将 $f(x)$ 图象的纵坐标不变, 横坐标变为原来的 2 倍, 再向右平移 $\frac{2 \pi}{3}$ 个单位长度, 得到的图象在 $[-\alpha, 2 \alpha]$ 上单调递增, 求 $\alpha$ 的取值范围;
(2) 若函数 $g(x)$ 在 $[0, \pi]$ 内恰有两个零点, 求 $a$ 的取值范围.
对于集合 $A=\left\{\theta_1, \theta_2, \cdots, \theta_n\right\}$ 和常数 $\theta_0$ ,定义: $\lambda=\frac{\cos ^2\left(\theta_1-\theta_0\right)+\cos ^2\left(\theta_2-\theta_0\right)+\cdots+\cos ^2\left(\theta_n-\theta_0\right)}{n}$ 为集合 $A$ 相对 $\theta_0$ 的 "余弦方差" 。
(1)若集合 $A=\left\{\frac{\pi}{5}, \frac{3 \pi}{10}\right\}, \theta_0=0$, 求集合 $A$ 相对 $\theta_0$ 的"余弦方差";
(2)求证:集合 $A=\left\{\frac{\pi}{3}, \frac{2 \pi}{3}, \pi\right\}$, 相对任何常数 $\theta_0$ 的 "余弦方差"是一个与 $\theta_0$ 无关的定值, 并求此定值;
(3)若集合 $A=\left\{\frac{\pi}{4}, \alpha, \beta\right\}, \alpha \in\left[-\frac{\pi}{2}, 0\right), \beta \in\left[\frac{\pi}{2}, \pi\right)$,集合 $A$ 相对任何常数 $\theta_0$ 的"余弦方差"是一个与 $\theta_0$ 无关的定值, 求出 $\alpha 、 \beta$.