如图所示, 在 $\triangle A B C$ 中, $P$ 在线段 $B C$ 上, 满足 $2 \overrightarrow{B P}=\overrightarrow{P C}, O$ 是线段 $A P$ 的中点.
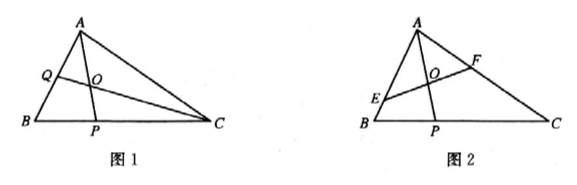
(1)延长 $C O$ 交 $A B$ 于点 $Q$ (如图1), 若4 $\overrightarrow{A B} \cdot \overrightarrow{A C}=15 \overrightarrow{A O} \cdot \overrightarrow{Q C}$, 求 $\frac{A C}{A B}$ 的值;
(2)过点 $O$ 的直线与边 $A B, A C$ 分别交于点 $E, F$ (如图2), 设 $\overrightarrow{E B}=\lambda \overrightarrow{A E}, \overrightarrow{F C}=\mu \overrightarrow{A F}$.
(i)求证: $2 \lambda+\mu$ 为定值;
(ii)设 $\triangle A E F$ 的面积为 $S_1, \triangle A B C$ 的面积为 $S_2$, 求 $\frac{S_1}{S_2}$ 的最小值.

(1)延长 $C O$ 交 $A B$ 于点 $Q$ (如图1), 若4 $\overrightarrow{A B} \cdot \overrightarrow{A C}=15 \overrightarrow{A O} \cdot \overrightarrow{Q C}$, 求 $\frac{A C}{A B}$ 的值;
(2)过点 $O$ 的直线与边 $A B, A C$ 分别交于点 $E, F$ (如图2), 设 $\overrightarrow{E B}=\lambda \overrightarrow{A E}, \overrightarrow{F C}=\mu \overrightarrow{A F}$.
(i)求证: $2 \lambda+\mu$ 为定值;
(ii)设 $\triangle A E F$ 的面积为 $S_1, \triangle A B C$ 的面积为 $S_2$, 求 $\frac{S_1}{S_2}$ 的最小值.