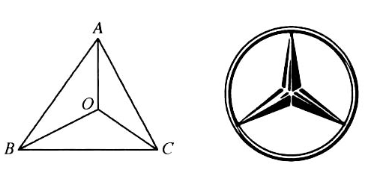
"奔驰定理" (若 $O$ 是 $\triangle A B C$ 内的一点, $\triangle B O C, \triangle A O C, \triangle A O B$ 的面积分别为 $S_A, S_B, S_C$, 则 $S_A$. $\overrightarrow{O A}+S_B \cdot \overrightarrow{O B}+S_C \cdot \overrightarrow{O C}=\overrightarrow{0}$ )是平面向量中一个非常优美的结论, 因为这个定理对应的图形与 "奔驰" 轿车 (Mercedes - Benz) 的标识很相似,故形象地称其为 "奔驰定理" . 若 $O$ 是锐角 $\triangle A B C$ 内的一点,则下列说法正确的有

A. 若 $A B=B C=C A=t$, 则 $O$ 到三边距离之和为定值 $\frac{\sqrt{3} t}{2}$
B. 若 $\overrightarrow{O A}+\overrightarrow{O B}+3 \overrightarrow{O C}=\overrightarrow{0}$, 则 $\triangle O A B$ 的面积与 $\triangle A B C$ 的面积之比为 $\frac{3}{5}$
C. 若 $\angle A B O=30^{\circ}, \angle A C O=60^{\circ}, \angle O B C=\angle O C B=15^{\circ}$, 则 $\tan \angle O A C=\frac{6-\sqrt{3}}{11}$
D. 若 $\overrightarrow{O A} \cdot \overrightarrow{O B}=\overrightarrow{O B} \cdot \overrightarrow{O C}=\overrightarrow{O C} \cdot \overrightarrow{O A}$, 则 $\tan A \cdot \overrightarrow{O A}+\tan B \cdot \overrightarrow{O B}+\tan C \cdot \overrightarrow{O C}=\overrightarrow{0}$