单选题 (共 8 题 ),每题只有一个选项正确
若全集 $\mathrm{U}=\mathbf{R}$, 集合 $A=\{x \mid 0 \leqslant x < 3\}, B=\{x \mid 1 < x < 4\}$, 则 $A \cap C_U B=$
$\text{A.}$ $[0,1)$
$\text{B.}$ $[0,1]$
$\text{C.}$ $(-\infty, 1)$
$\text{D.}$ $(-\infty, 1]$
复数 $z=\frac{3+4 \mathrm{i}}{2-\mathrm{i}}$ (其中 i 为虚数单位) 的共轭复数 $\bar{z}$ 在复平面内对应的点在
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知向量 $\vec{a}, \vec{b}$, 满足 $|\vec{a}|=2,(4 \vec{a}+\vec{b}) \cdot \vec{b}=4$, 则 $|2 \vec{a}+\vec{b}|=$
$\text{A.}$ $2 \sqrt{5}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ 20
$\text{D.}$ 5
若 $\sin (\pi-\alpha)=\frac{4}{5}, \alpha$ 为第二象限角, 则 $\sin 2 \alpha=$
$\text{A.}$ $-\frac{7}{25}$
$\text{B.}$ $-\frac{24}{25}$
$\text{C.}$ $\frac{7}{25}$
$\text{D.}$ $\frac{24}{25}$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右顶点为 $A$, 若以点 $A$ 为圆心, 以 $b$ 为半径的圆与 $C$ 的一条渐近线交于 $M, N$ 两点, 且 $\overrightarrow{O M}=-3 \overrightarrow{O N}$, 则 $C$ 的离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\frac{\sqrt{6}}{2}$
$\text{D.}$ $\frac{2 \sqrt{3}}{3}$
若曲线 $y=\ln (x+2 a)$ 的一条切线为 $y=\mathrm{e} x-2 b$ ( e 为自然对数的底数), 其中 $a, b$ 为正实数, 则 $\frac{1}{\mathrm{e} a}+\frac{1}{b}$ 的取值范围是
$\text{A.}$ $[2, \mathrm{e})$
$\text{B.}$ $(\mathrm{e}, 4]$
$\text{C.}$ $[4,+\infty)$
$\text{D.}$ $[e,+\infty)$
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 则
$\text{A.}$ 若 $\left\{a_n\right\}$ 为等差数列, 且 $S_9>S_8, S_9>S_{10}$, 则 $S_{17}>0, S_{18} < 0$
$\text{B.}$ 若 $\left\{a_n\right\}$ 为等差数列, 且 $S_{17}>0, S_{18} < 0$, 则 $a_{17}>0, a_{18} < 0$
$\text{C.}$ 若 $\left\{a_n\right\}$ 为等比数列, 且 $a_4>0$, 则 $\mathrm{S}_{2024}>0$
$\text{D.}$ 若 $\left\{a_n\right\}$ 为等比数列, 且 $a_5>0$, 则 $\mathrm{S}_{2023}>0$
已知奇函数 $f(x)$ 的定义域为 $\mathbf{R}$, 对任意的 $x$ 满足 $f(-x)=f(x+2)$, 且 $f(x)$ 在区间 $(-1,0)$ 上单调递增, 若 $a=\log _4 3, b=\log _\pi 2, c=\frac{1}{4} \log _{\sqrt{2}} 512 \sqrt{2}$, 则 $f(a), f(b), f(c)$ 的大小关系为
$\text{A.}$ $f(c)>f(a)>f(b)$
$\text{B.}$ $f(c)>f(b)>f(a)$
$\text{C.}$ $f(a)>f(b)>f(c)$
$\text{D.}$ $f(a)>f(c)>f(b)$
多选题 (共 3 题 ),每题有多个选项正确
下列论述正确的有
$\text{A.}$ 若 $A, B$ 两组成对数据的样本相关系数分别为 $r_A=0.97, r_B=-0.99$, 则 $A$ 组数据比 $B$ 组数据的相关性较强
$\text{B.}$ 数据 $49,21,32,29,38,65,30,50$ 的第 60 百分位数为 38
$\text{C.}$ 若随机变量 $X \sim N\left(7, \sigma^2\right)$, 且 $P(X>9)=0.12$, 则 $P(5 < X < 7)=0.38$
$\text{D.}$ 若样本数据 $x_1, x_2, \cdots, x_6$ 的方差为 1 , 则数据 $2 x_1-1,2 x_2-1, \cdots, 2 x_6-1$ 的方差为 4
已知函数 $f(x)=\min \{\sin x, \cos x\}$, 则
$\text{A.}$ $f(x)$ 关于直线 $x=-\frac{\pi}{4}$ 对称
$\text{B.}$ $f(x)$ 的最大值为 $\frac{\sqrt{2}}{2}$
$\text{C.}$ $f(x)$ 在 $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ 上不单调
$\text{D.}$ 在 $(0,2 \pi)$, 方程 $f(x)=m$ ( $m$ 为常数) 最多有 4 个解
已知圆 $O: x^2+y^2=r^2(r>0)$, 斜率为 $k$ 的直线 $l$ 经过圆 $O$ 内不在坐标轴上的一个定点 $P$, 且与圆 $O$相交于 $A 、 B$ 两点, 下列选项中正确的是
$\text{A.}$ 若 $r$ 为定值, 则存在 $k$, 使得 $O P \perp A B$
$\text{B.}$ 若 $k$ 为定值, 则存在 $r$, 使得 $O P \perp A B$
$\text{C.}$ 若 $r$ 为定值, 则存在 $k$, 使得圆 $O$ 上恰有三个点到 $l$ 的距离均为 $|k|$
$\text{D.}$ 若 $k$ 为定值, 则存在 $r$, 使得圆 $O$ 上恰有三个点到 $l$ 的距离均为 $\frac{r}{2}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
设椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左. 右焦点分别为 $F_1, F_2, P$ 是 $C$ 上的点 $P F_2 \perp F_1 F_2, \angle P F_1 F_2=30^{\circ}$, 则 $C$ 的离心率为
已知正三棱锥 $P-A B C$, 点 $P, A, B, C$ 都在半径为 $\sqrt{3}$ 的球面上, 若 $P A, P B, P C$ 两两相互垂直, 则球心到截面 $A B C$ 的距离为
$\triangle A B C$ 为锐角三角形, 其三个内角 $A 、 B、 C$ 的对边分别为 $a, b ,c$, 且 $b=1, C=2 B$, 则 $\triangle A B C$ 周长的取值范围为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
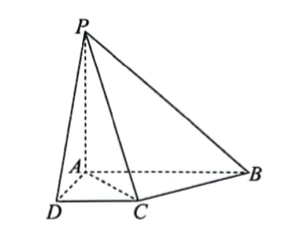
如图, 四棱锥 $P-A B C D$ 中, $P A \perp$ 底面 $A B C D, A B / / C D, A D=C D=a, \angle B A D=120^{\circ}$, $\angle A C B=90^{\circ}$.
(1)求证: $B C \perp$ 平面 $P A C$;
(2)若 $P A=\sqrt{3} a$, 求二面角 $D-P C-A$ 的余弦值.
第 33 届夏季奥林匹克运动会运动会于 2024 年 7 月 26 日至 8 月 11 日在法国巴黎举行, 共设置射击、游泳、田径、篮球等 32 个大项,329 个小项.共有来自 120 多个国家的近万名运动健儿同台竞技.我国也将派出强大的阵容在多个项目上参与奖牌的争夺. 武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动, 努力让大家更多的了解奥运会的相关知识. 武汉市体育局为了解广大民众对奥运会知识的知晓情况, 在全市开展了网上问卷调查, 民众参与度极高, 现从大批参与者中随机抽取 200 名幸运参与者, 他们得分(满分 100 分) 数据, 统计结果如下:

(1) 若此次问卷调查得分整体服从正态分布, 用样本来估计总体, 设 $\mu, \sigma$ 分别为这 200 人得分的平均值和标准差(同一组数据用该区间中点值作为代表), 求 $\mu, \sigma$ 的值 ( $\mu, \sigma$ 的值四舍五入取整数) 并计算 $P(51 < X < 93)$;
(2)在 (1) 的条件下, 为感谢大家参与这次活动, 市体育局还对参加问卷调查的幸运市民制定如下奖励方案: 得分低于 $\mu$ 的可以获得 1 次抽奖机会, 得分不低于 $\mu$ 的可获得 2 次抽奖机会, 在一次抽奖中, 抽中价值为 15 元的纪念品 $A$ 的概率为 $\frac{2}{3}$, 抽中价值为 30 元的纪念品 $B$ 的概率为 $\frac{1}{3}$. 现有市民张先生参加了此次问卷调查并成为幸运参与者, 记 $Y$ 为他参加活动获得纪念品的总价值, 求 $Y$ 的分布列和数学期望.
(参考数据: $P(\mu-\sigma < X \leqslant \mu+\sigma) \approx 0.6827, P(\mu-2 \sigma < X \leqslant \mu+2 \sigma) \approx 0.9545$,
$$
P(\mu-3 \sigma < X \leqslant \mu+3 \sigma) \approx 0.9973)
$$
已知曲线 $C$ 上的点到点 $F(-1,0)$ 的距离比到直线 $x=3$ 的距离小 $2, O$ 为坐标原点.直线 $l$ 过定点 $A(0,1)$.
(1) 直线 $l$ 与曲线 $C$ 仅有一个公共点, 求直线 $l$ 的方程;
(2) 曲线 $C$ 与直线 $l$ 交于 $M, N$ 两点, 试分别判断直线 $O M, O N$ 的斜率之和、斜率之积是否为定值? 并说明理由.
已知函数 $f(x)=x-\frac{1}{a} \ln x$ 与函数 $g(x)=\mathrm{e}^{a x}-x$, 其中 $a>0$
(1) 求 $f(x)$ 的单调区间;
(2)若 $g(x)>0$, 求 $a$ 的取值范围;
(3) 若曲线 $y=f(x)$ 与 $x$ 轴有两个不同的交点, 求证: 曲线 $y=f(x)$ 与曲线 $y=g(x)$ 共有三个不同的交点.
定义: 在一个有穷数列的每相邻两项之间插入这两项的和, 形成新的数列, 我们把这样的操作称为该数列的一次 “和扩充”,例如:数列1,2,3 经过第一次 “和扩充” 后得到数列1,3,2,5,3 ; 第二次 “和扩充”后得到数列 $1,4,3,5,2,7,5,8,3$. 设数列 $a, b, c$ 经过 $n$ 次 “和扩充” 后得到的数列的项数为 $P_n$, 所有项的和为 $S_n$.
(1) 若 $a=2, b=3, c=4$, 求 $P_2, S_2$;
(2)若 $P_n \geq 2024$, 求正整数 $n$ 的最小值;
(3) 是否存在数列 $a, b, c(a, b, c \in \mathbf{R})$, 使得数列 $\left\{S_n\right\}$ 为等比数列? 请说明理由.