单选题 (共 8 题 ),每题只有一个选项正确
复数 $2 \mathrm{i}(3-\mathrm{i})$ 的共轭复数为
$\text{A.}$ $2+6 \mathrm{i}$
$\text{B.}$ $2-6 \mathrm{i}$
$\text{C.}$ $-2+6 \mathrm{i}$
$\text{D.}$ $-2-6 \mathrm{i}$
已知集合 $A=\{2 a-1, a, 3\}, B=\left\{x \mid x^2-3 x+2=0\right\}$, 若 $A \cap B \neq \varnothing$, 则 $a=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ -1
已知 $f(x)$ 是定义在 $\mathbf{R}$ 上的奇函数, 且当 $x \geqslant 0$ 时, $f(x)=2^x+x+m$, 则 $f(-3)=$
$\text{A.}$ -10
$\text{B.}$ -4
$\text{C.}$ 4
$\text{D.}$ 10
已知 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 是抛物线 $C: x^2=8 y$ 上的两点, 且直线 $A B$ 经过 $C$ 的焦点, 若 $y_1+$ $y_2=12$, 则 $|A B|=$
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 16
$\text{D.}$ 18
已知 $f^{\prime}(x)$ 是函数 $f(x)$ 的导函数, 若函数 $y=\mathrm{e}^{f(x)}$ 的图象大致如图所示, 则 $f(x)$ 的极大值点为
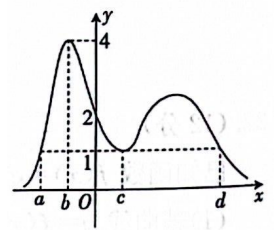
$\text{A.}$ $a$
$\text{B.}$ $b$
$\text{C.}$ $c$
$\text{D.}$ $d$
在四面体 $A B C D$ 中, $A B \perp B C, A B=1, A D=C D=2 \sqrt{2}, B C=\sqrt{15}$, 则四面体 $A B C D$ 外接球的体积为
$\text{A.}$ $16 \pi$
$\text{B.}$ $\frac{16 \pi}{3}$
$\text{C.}$ $32 \pi$
$\text{D.}$ $\frac{32 \pi}{3}$
某工厂新购置并安装了先进的废气处理设备, 使产生的废气经过该设备过滤后排放, 以减少对空气的污染. 已知过滤过程中废气的污染物数量 $P$ (单位: $\mathrm{mg} / \mathrm{L}$ ) 与过滤时间 $t$ (单位; $\mathrm{h}$ ) 的关系为 $P(t)=P_0 \mathrm{e}^{-k t}\left(P_0, k\right.$ 是正常数). 若经过 $10 \mathrm{~h}$ 过波后减少了 $20 \%$ 的污染物, 在此之后为了使得污染物减少到原来的 $10 \%$ 还需要的时长大约为(参考数据: $\log _2 5 \approx 2.322$ )
$\text{A.}$ $103 \mathrm{~h}$
$\text{B.}$ $93 \mathrm{~h}$
$\text{C.}$ $83 \mathrm{~h}$
$\text{D.}$ $63 \mathrm{~h}$
已知 $a>0, b>1$, 且 $\mathrm{e}^{2 a}+2 \ln b+1=b^2+2 a$, 则必有
$\text{A.}$ $b>\mathrm{e}^a$
$\text{B.}$ $\ln b < a$
$\text{C.}$ $a+\ln b=1$
$\text{D.}$ $a+\ln b < 1$
多选题 (共 4 题 ),每题有多个选项正确
若点 $P(1,0)$ 在圆 $C: x^2+y^2+2 x+4 y+m=0$ 的外部, 则 $m$ 的取值可能为
$\text{A.}$ -3
$\text{B.}$ 1
$\text{C.}$ 4
$\text{D.}$ 7
某地发起“寻找绿色合伙人一一低碳生活知识竞赛”活动, 选取了 $n$ 人参与问卷调查, 将他们的成绩进行适当分组后 (每组为左闭右开的区间), 得到如图所示的频率分布直方图,且成绩落在 $[90,100)$ 的人数为 10 , 则
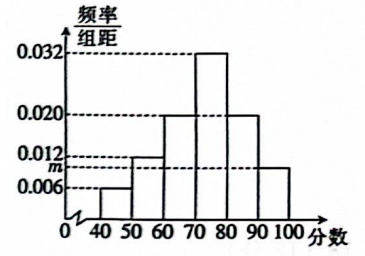
$\text{A.}$ $m=0.01$
$\text{B.}$ $n=100$
$\text{C.}$ 若同一组中的数据用该组区间的中点值作代表, 则问卷调查成绩的平均数低于 70
$\text{D.}$ 问卷调查成绩的 $80 \%$ 分位数的估计值为 85
若数列 $\left\{c_n\right\}$ 满足 $c_{n+1}=c_n^2$, 则称 $\left\{c_n\right\}$ 为 “平方递推数列”. 已知数列 $\left\{a_n\right\}$ 是 “平方递推数列”, 且 $a_1>0, a_1 \neq 1$, 则
$\text{A.}$ $\left\{\lg a_n\right\}$ 是等差数列
$\text{B.}$ $\left\{\lg a_n\right\}$ 是等比数列
$\text{C.}$ $\left\{a_n a_{n+1}\right\}$ 是 “平方递推数列”
$\text{D.}$ $\left\{a_{n+1}+a_n\right\}$ 是 “平方递推数列”
某数学学习小组甲、乙、丙三人分别构建了如图所示的正四棱台(1), (2), (3), 从左往右, 若上底面边长、下底面边长、高均依次递增 $d \mathrm{~cm}$, 记正四棱台(1), (2), (3)的侧棱与底面所成的角分别为 $\alpha_1, \alpha_2, \alpha_3$, 正四棱台(1),(2),(3)的侧面与底面所成的角分别为 $\theta_1, \theta_2, \theta_3$, 则

$\text{A.}$ $\sin \alpha_1+\sin \alpha_3=2 \sin \alpha_2$
$\text{B.}$ $\tan \alpha_1+\tan \alpha_3=2 \tan \alpha_2$
$\text{C.}$ $\cos \theta_1+\cos \theta_3=2 \cos \theta_2$
$\text{D.}$ $\tan \theta_1+\tan \theta_3=2 \tan \theta_2$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $\boldsymbol{a}=(x, 2), \boldsymbol{b}=(3,4)$, 若 $(\boldsymbol{a}+\boldsymbol{b}) \perp \boldsymbol{b}$, 则 $x=$
一排 6 个座位坐了 2 个三口之家, 若同一家人座位相邻, 则不同的坐法种数为 (用数字作答)
已知函数 $f(x)=2 \sin \omega x+1(\omega>0)$ 在 $[0, \pi]$ 上有且仅有 2 个零点, 则 $\omega$ 的取值范围为
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点为 $F$, 直线 $l: 3 x+4 y=0$ 与 $C$ 相交于 $A, B$两点, 若 $|A B|=2|O F|$ ( $O$ 为坐标原点), 则 $C$ 的离心率为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $c \cos A-a \cos B+c=0$.
(1) 求 $\sin ^2 B+\sin ^2 C-\sin ^2 A$ 的值;
(2)若 $a=5$, 求 $\triangle A B C$ 面积的最大值.
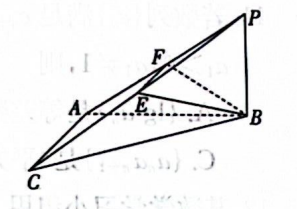
如图, 在三棱椎 $P-A B C$ 中, $P B \perp$ 平面 $A B C, A B \perp A C, E, F$ 分别为 $P C, P A$ 的中点, 且 $B P$ $=2 \sqrt{3}, A B=3 \sqrt{3}, B C=6$.
(1)证明: 平面 $B E F \perp$ 平面 $P A B$.
(2) 求平面 $B E F$ 与平面 $P E B$ 夹角的余弦值.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_n+4=2 a_n$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 求数列 $\left\{\frac{n+2}{n(n+1) a_{n+1}}\right\}$ 的前 $n$ 项和 $T_n$.
为了促进消费, 某商场针对会员客户推出会员积分兑换商品活动: 每位会员客户可在价值 80 元, 90 元, 100 元的 $A, B, C$ 三种商品中选择一种使用积分进行兑换,每 10 积分可兑换 1 元. 已知参加活动的甲、乙两位客户各有 1000 积分,且甲兑换 $A, B, C$ 三种商品的概率分别为 $\frac{1}{2}, \frac{1}{3}, \frac{1}{6}$, 乙兑换 $A, B, C$ 三种商品的概率分别为 $\frac{1}{2}, \frac{1}{6}, \frac{1}{3}$, 且他们兑换何种商品相互独立.
(1)求甲、乙两人兑换同一种商品的概率;
(2)记 $X$ 为两人兑换商品后的积分总余额,求 $X$ 的分布列与期望.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的焦距为 $2 \sqrt{3}$, 且 $\frac{b^2}{a^2}+\frac{a^2}{b^2}=\frac{17}{4}$.
(1)求 $C$ 的方程;
(2) $A$ 是 $C$ 的下顶点, 过点 $P(4,0)$ 的直线 $l$ 与 $C$ 相交于 $M, N$ 两点,直线 $l$ 的斜率小于 0 , $\triangle A M N$ 的重心为 $G, O$ 为坐标原点, 求直线 $O G$ 斜率的最大值.
已知函数 $f(x)=\mathrm{e}^x+a x^2$.
(1) 若曲线 $y=f(x)$ 在点 $(1, f(1))$ 处的切线经过坐标原点, 求 $a$ 的值;
(2) 若关于 $x$ 的方程 $f(x)=x+1$ 恰有 2 个不同的实数根, 求 $a$ 的取值范围.