陕西西安市蓝田高二上月考试卷

导出试卷

陕西西安市蓝田高二上月考试卷

一、单选题（共 8 题），每题只有一个选项正确

1. 已知

\vec{a} = (- 1, 3, - 2), \vec{b} = (1, - 1, m)

, 且

\vec{a} \cdot \vec{b} = - 2

, 则

m =

A.

- 1

B.

1

C.

- 2

D.

2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 已知直线

a x + b y - 1 = 0

在

y

轴上的截距为 -1 , 且它的倾斜角为

\frac{π}{4}

, 则

a - b =

A.

B.

C.

-2

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 已知常数

a, b \in R

, 且

a, b

不全为零, 若直线

a x + b y = 1

与圆

C : x^{2} + y^{2} = 1

相交, 则点

P (a, b)

与圆

C

的位置关系是

A.

点在圆内

B.

点在圆上

C.

点在圆外

D.

随

a 、 b

取值的变化而变化

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

\sqrt{(x - a)^{2} + (y - b)^{2}}

可以转化为平面上

M (x, y)

点与点

N (a, b)

之间的距离. 结合上述观点, 可得

f (x) = \sqrt{x^{2} + 8 x + 20} + \sqrt{x^{2} + 4 x + 20}

的最小值为

A.

\sqrt{29}

B.

2 \sqrt{10}

C.

\sqrt{31}

D.

2 + \sqrt{13}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

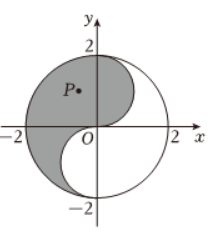
5. “太极图”因其形状如对称的阴阳两鱼互抱在一起, 故也被称为“阴阳鱼太极图”. 如图是放在平面直角坐标系中的“太极图”, 图中曲线为圆或半圆, 已知点

P (x, y)

是阴影部分 (包括边界) 的动点, 则

\frac{y}{x - 2}

的最小值为

A.

- \frac{2}{3}

B.

- \frac{3}{2}

C.

- \frac{4}{3}

D.

- 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

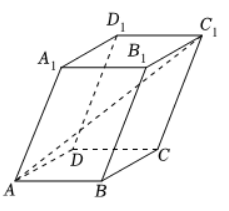
6. 如图, 平行六面体

A B C D - A_{1} B_{1} C_{1} D_{1}

的底面

A B C D

是矩形, 其中

A B = 2, A D =

4, A A_{1} = 3

, 且

∠ A_{1} A D = ∠ A_{1} A B = 60^{\circ}

, 则线段

A C_{1}

的长为

A.

9

B.

\sqrt{29}

C.

\sqrt{47}

D.

4 \sqrt{3}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知正三棱柱

A B C - A_{1} B_{1} C_{1}

的侧棱长为 3 , 底面边长为 2 , 则直线

A B_{1}

与侧面

A C C_{1} A_{1}

所成角的正弦值等于

A.

\frac{\sqrt{39}}{13}

B.

\frac{\sqrt{130}}{13}

C.

\frac{\sqrt{2}}{2}

D.

\frac{\sqrt{3}}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 汉代初年成书的《淮南万毕术》记载: “取大镜高悬, 置水盆于下, 则见四邻矣”. 这是中国古代人民利用平面镜反射原理的首个实例, 体现了传统文化中的数学智慧. 在平面直角坐标系

x O y

中, 一条光线从点

(- 2, 0)

射出, 经

y

轴反射后的光线所在的直线与圆

x^{2} + y^{2} - 2 x - 2 y = 0

相切, 则反射光线所在直线的斜率为

A.

-1

B.

-1 或 1

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 4 题），每题有多个选项正确

9. 关于直线

l : x + \sqrt{3} y + 2 = 0

, 下列说法正确的有

A.

斜率为

\sqrt{3}

B.

倾斜角为

150^{\circ}

C.

在

x

轴上的截距为 -2

D.

直线

l

不经过第一象限

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 已知三条直线

2 x - 3 y + 1 = 0, 4 x + 3 y + 5 = 0, m x - y - 1 = 0

不能构成三角形, 则实数

m

的取值可以是

A.

- \frac{4}{3}

B.

- \frac{2}{3}

C.

\frac{2}{3}

D.

2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 下列说法正确的是

A.

若空间中的

O, A, B, C

满足

\vec{O C} = \frac{1}{3} \vec{O A} + \frac{2}{3} \vec{O B}

, 则

A, B, C

三点共线

B.

空间中三个向量

\vec{a}, \vec{b}, \vec{c}

, 若

\vec{a} / / \vec{b}

, 则

\vec{a}, \vec{b}, \vec{c}

共面

C.

对空间任意一点

O

和不共线的三点

A, B, C

, 若

\vec{O P} = 2 \vec{O A} + 2022 \vec{O B} - 2023 \vec{O C}

, 则

P, A, B, C

四点共面

D.

设

{\vec{a}, \vec{b}, \vec{c}}

是空间的一组基, 若

\vec{m} = \vec{a} + \vec{b}, \vec{n} = \vec{a} - \vec{b}

, 则

{\vec{m}, \vec{n}, \vec{c}}

不能为空间的一组基

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 已知圆

C : x^{2} + y^{2} - 4 x + 2 = 0

, 则下列说法正确的有

A.

直线

x - y - 1 = 0

与圆

C

的相交弦长为

\sqrt{6}

B.

圆

C

关于直线

x - y = 0

对称的圆的方程为

x^{2} + (y - 2)^{2} = 2

C.

若点

P (x, y)

是圆

C

上的动点, 则

x^{2} + y^{2}

的最大值为

2 + \sqrt{2}

D.

若圆

C

上有且仅有三个点到直线

x + y + m = 0

的距离等于

\frac{\sqrt{2}}{2}

, 则

m = - 1

或

- 3

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 4 题），请把答案直接填写在答题纸上

13. 已知向量

\vec{a} = (2, - 1, 3), \vec{b} = (- 4, 2, t)

的夹角为钝角, 则实数

t

的取值范围为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 已知点

(1, - 1)

关于直线

l_{1} : y = 2 x

的对称点为

A

, 设直线

l_{2}

经过点

A

, 则当点

B (2, - 1)

到直线

l_{2}

的距离最大时, 直线

l_{2}

的方程是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 在平面直角坐标系中, 动点

P

到两条直线

3 x - y = 0

与

x + 3 y = 0

的距离之和等于 4 , 则点

P

到原点距离的取值范围为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 已知圆

E

的圆心为

(a, 2)

, 直线

l_{1} : x - y + 1 = 0, l_{2} : x - y - 1 = 0

与圆

E

分别交于点

A, B

与

C, D

, 若四边形

A B

C D

是正方形, 则圆

E

的标准方程为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

17. 已知直线

l : 2 x - 3 y + 1 = 0

, 点

A (- 1, - 2)

. 求:
(1) 点

A

关于直线

l

的对称点

A^{'}

的坐标;
(2) 直线

m : 3 x - 2 y - 6 = 0

关于直线

l

的对称直线

m^{'}

的方程;
(3) 直线

l

关于点

A

对称的直线

l^{'}

的方程.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 求满足下列条件的直线的方程:
(1) 直线

l

经过两条直线

2 x + y - 8 = 0

和

x - 2 y + 1 = 0

的交点, 且平行于直线

4 x - 3 y - 7 = 0

. 求直线

l

的方程;
(2) 已知

△ A B C

的顶点

A (5, 1)

, 边

A B

上的中线

C M

所在直线方程为

2 x - y - 5 = 0

, 边

A C

上的高

B H

所在直线方程为

x - 2 y - 5 =

0 , 求直线

B C

的方程.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

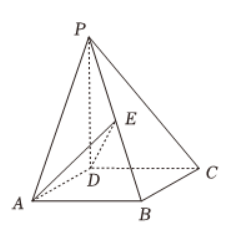
19. 已知四棱雉

P - A B C D

中, 底面

A B C D

是正方形,

P D ⊥

平面

A B C D, P D = A

B = 1, E

是

P B

的中点.
(1) 求直线

B D

与直线

P C

所成角的余弦值;
(2) 求证:

P C ⊥

平面

A D E

;
(3) 求点

B

到平面

A D E

的距离.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 已知

x^{2} + y^{2} - 4 x + 2 m y + 2 m^{2} - 2 m + 1 = 0 (m \in R)

表示圆

C

的方程.
(1) 求实数

m

的取值范围;
(2) 当圆

C

的面积最大时, 求过点

A (4, - 4)

圆的切线方程;
(3)

P

为圆上任意一点, 已知

B (6, 0)

, 在 (2) 的条件下, 求

| P A |^{2} + | P B |^{2}

的最小值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

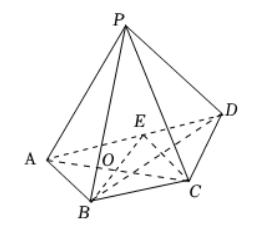
21. 如图所示, 在四棱椎

P - A B C D

中,

P A ⊥

平面

P C D

, 底面

A B C D

满足

A D / / B C, A P = A B

= B C = \frac{1}{2} A D = 4, ∠ A B C = 90^{\circ}, E

为

A D

的中点,

A C

与

B E

的交点为

O

.
(1) 设

H

是线段

B E

上的动点, 证明: 三棱椎

H - P C D

的体积是定值；
(2) (文科生做) 求四棱椎

P - A B C D

的体积.
(理科生做) 求直线

B C

与平面

P B D

所成角的余弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。