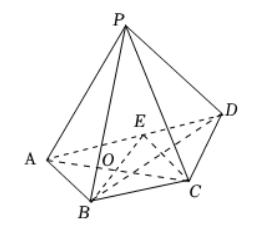
如图所示, 在四棱椎 $P-A B C D$ 中, $P A \perp$ 平面 $P C D$, 底面 $A B C D$ 满足 $A D / / B C, A P=A B$ $=B C=\frac{1}{2} A D=4, \angle A B C=90^{\circ}, E$ 为 $A D$ 的中点, $A C$ 与 $B E$ 的交点为 $O$.
(1) 设 $H$ 是线段 $B E$ 上的动点, 证明: 三棱椎 $H-P C D$ 的体积是定值；
(2) (文科生做) 求四棱椎 $P-A B C D$ 的体积.
(理科生做) 求直线 $B C$ 与平面 $P B D$ 所成角的余弦值.