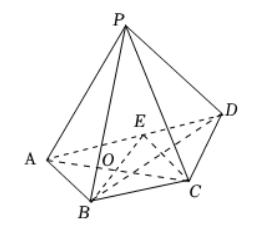
如图所示, 在四棱椎
(1) 设
(2) (文科生做) 求四棱椎
(理科生做) 求直线
(1) 设
(2) (文科生做) 求四棱椎
(理科生做) 求直线
