单选题 (共 12 题 ),每题只有一个选项正确
设复数 $\mathrm{z}$ 满足 $\frac{1+\mathrm{z}}{1-\mathrm{z}}=\mathrm{i}$, 则 $|\mathrm{z}|=(\mathrm{O})$
$\text{A.}$ $1$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $2$
$\sin 20^{\circ} \cos 10^{\circ}-\cos 160^{\circ} \sin 10^{\circ}=$ ( )
$\text{A.}$ $-\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $\frac{1}{2}$
设命题 $p: \exists n \in N, n^{2}>2^{n}$, 则 $\neg p$ 为 ( )
$\text{A.}$ $\forall n \in N, n^{2}>2^{n}$
$\text{B.}$ $\exists n \in N, n^{2} \leqslant 2^{n}$
$\text{C.}$ $\forall \mathrm{n} \in \mathrm{N}, \mathrm{n}^{2} \leqslant 2^{\mathrm{n}}$
$\text{D.}$ $\exists n \in N, n^{2}=2^{n}$
投篮测试中, 每人投 3 次, 至少投中 2 次才能通过测试. 已知某同 学每次投篮投中的概率为 $0.6$, 且各次投篮是否投中相互独立, 则该同学通过 测试的概率为
$\text{A.}$ $0.648$
$\text{B.}$ $0.432$
$\text{C.}$ $0.36$
$\text{D.}$ $0.312$
已知 $M\left(x_{0}, y_{0}\right)$ 是双曲线 $C: \frac{x^{2}}{2}-y^{2}=1$ 上的一点, $F_{1}, F_{2}$ 是 $C$ 的左、 右两个焦点, 怘 $\overrightarrow{\mathrm{MF}_{1}} \cdot \overrightarrow{\mathrm{MF}_{2}} < 0$, 则 $\mathrm{y}_{0}$ 的取值范围是( )
$\text{A.}$ $\left(\frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3}\right)$
$\text{B.}$ $\left(\frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}\right)$
$\text{C.}$ $\left(-\frac{2 \sqrt{2}}{3}, \frac{2 \sqrt{2}}{3}\right)$
$\text{D.}$ $\left(-\frac{2 \sqrt{3}}{3}, \frac{2 \sqrt{3}}{3}\right)$
6. (5 分) 《九章算术》是我国古代内容极为丰富的数学名著, 书中有如下问 题:"今有委米依垣内角, 下周八尺, 高五尺. 问:积及为米几何? “其意思 为: "在屋内墙角处堆放米(如图, 米堆为一个圆锥的四分之一), 米堆底部 的弧长为 8 尺, 米堆的高为 5 尺, 问米堆的体积和堆放的米各为多少? “已知 1 斛米的体积约为 $1.62$ 立方尺, 圆周率约为 3 , 估算出堆放的米约有 ( )
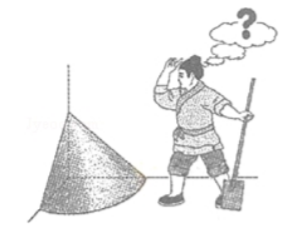
$\text{A.}$ 14 斛
$\text{B.}$ 22 斛
$\text{C.}$ 36 斛
$\text{D.}$ 66 斛
设 $\mathrm{D}$ 为 $\triangle \mathrm{ABC}$ 所在平面内一点, $\overrightarrow{\mathrm{BC}}=3 \overrightarrow{\mathrm{CD}}$, 则 ( )
$\text{A.}$ $\overrightarrow{\mathrm{AD}}=-\frac{1}{3} \overrightarrow{\mathrm{AB}}+\frac{4}{3} \overrightarrow{\mathrm{AC}}$
$\text{B.}$ $\overrightarrow{\mathrm{AD}}=\frac{1}{3} \overrightarrow{\mathrm{AB}}-\frac{4}{3} \overrightarrow{\mathrm{AC}}$
$\text{C.}$ $\overrightarrow{\mathrm{AD}}=\frac{4}{3} \overrightarrow{\mathrm{AB}}+\frac{1}{3} \overrightarrow{\mathrm{AC}}$
$\text{D.}$ $\overrightarrow{\mathrm{AD}}=\frac{4}{3} \overrightarrow{\mathrm{AB}}-\frac{1}{3} \overrightarrow{\mathrm{AC}}$
函数 $f(x)=\cos (\omega x+\phi)$ 的部分图象如图所示, 则 $f(x)$ 的单调递
减区间为
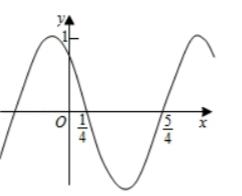
$\text{A.}$ $\left(k \pi-\frac{1}{4}, k \pi+\frac{3}{4}\right), k \in z$
$\text{B.}$ $\left(2 k \pi-\frac{1}{4}, 2 k \pi+\frac{3}{4}\right), k \in z$
$\text{C.}$ $\left(k-\frac{1}{4}, k+\frac{3}{4}\right), k \in z$
$\text{D.}$ $\left(2 k-\frac{1}{4}, 2 k+\frac{3}{4}\right), k \in z$
执行如图所示的程序框图,如果输入的 $t=0.01$,则输出的 $n=$
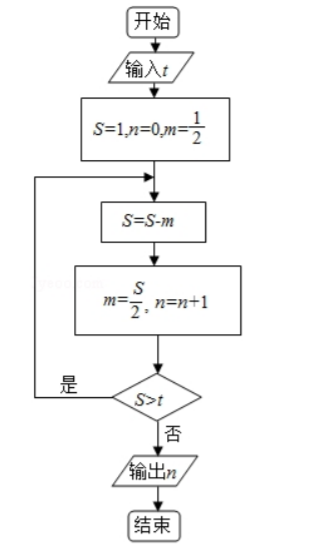
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 7
$\text{D.}$ 8
$\left(x^{2}+x+y\right)^{5}$ 的展开式中, $x^{5} y^{2}$ 的系数为 ( )
$\text{A.}$ 10
$\text{B.}$ 20
$\text{C.}$ 30
$\text{D.}$ 60
圆柱被一个平面截去一部分后与半球(半径为 $r$ )组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示. 若该几何体的表面积为
$16+20 \pi$ 则 $ r=$
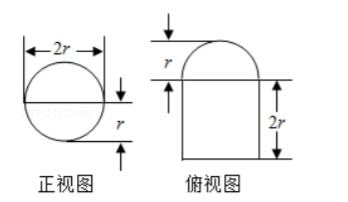
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ 5
设函数 $f(x)=e^{x}(2 x-1)-a x+a$, 其中 $a < 1$, 若存在唯一的整数 $x_{0}$ 使得 $f\left(x_{0}\right) < 0$, 则 $a$ 的取值范围是
$\text{A.}$ $\left[-\frac{3}{2 \mathrm{e}}, 1\right)$
$\text{B.}$ $\left[-\frac{3}{2 e}, \frac{3}{4}\right)$
$\text{C.}$ $\left[\frac{3}{2 \mathrm{e}}, \frac{3}{4}\right)$
$\text{D.}$ $\left[\frac{3}{2 \mathrm{e}}, 1\right)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若函数 $f(x)=x \ln \left(x+\sqrt{a+x^{2}}\right)$ 为偶函数, 则 $a=$
一个圆经过椭圆 $\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$ 的三个顶点. 且圆心在 $x$ 轴的正半轴上. 则该圆标准方程为
若$ x, y$ 满足约束条件
$$
\left\{\begin{array}{l}
x-1 \geqslant 0 \\
x-y \leqslant 0 \\
x+y-4 \leqslant 0
\end{array}\right.
$$
则 $ \dfrac{y}{x}$ 的最大值为
在平面四边形 $A B C D$ 中, $\angle A=\angle B=\angle C=75^{\circ}$. $B C=2$, 则 $A B$ 的取值范 围是
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\mathrm{S}_{\mathrm{n}}$ 为数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, 已知 $a_{n}>0, a_{n}^{2}+2 a_{n}=4 S_{n}+3$
(1) 求 $\left\{a_{n}\right\}$ 的通项公式:
(II) 设 $b_{n}=\frac{1}{a_{n} a_{n+1}}$, 求数列 $\left\{b_{n}\right\}$ 的前 $n$ 项和.
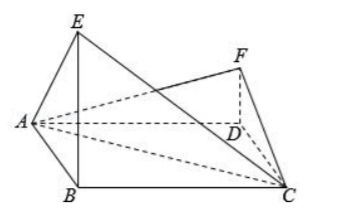
如图, 四边形 $A B C D$ 为菱形, $\angle A B C=120^{\circ}, E, F$ 是平面 $A B C D$ 同一侧的两点, $B E$ 上平面 $A B C D, D F$ 上平面 $A B C D, B E=2 D F, A E \perp E C$.
(I ) 证明: 平面 $A E C \perp$ 平面 $A F C$
(II) 求直线 $\mathrm{AE}$ 与直线 $\mathrm{CF}$ 所成角的余弦值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 $x$(单位: 千元) 对年销售量 y(单位: t) 和年利润 z(单位: 千元) 的影响, 对近 8 年的年宣传费 $x_{i}$ 和年销售量 $y_{i}(i=1,2, \ldots, 8)$ 数据作了初步处理, 得 到下面的散点图及一些统计量的值.

表中 $w_{i}=\sqrt{x}, \quad-\frac{1}{8} \sum_{i=1}^{8} w_{i}$
( I ) 根据散点图判断, $y=a+b x$ 与 $y=c+d \sqrt{x}$ 哪一个适宜作为年销售量 $y$ 关于年宣 传费 $\mathrm{x}$ 的回归方程类型? (给出判断即可, 不必说明理由)
(II )根据(I )的判断结果及表中数据, 建立 $\mathrm{y}$ 关于 $\mathrm{x}$ 的回归方程;
(III) 已知这种产品的年利润 $z$ 与 $x 、 y$ 的关系为 $z=0.2 y-x$. 根据(II ) 的结果 回答下列问题:
(i)年宣传费 $x=49$ 时, 年销售量及年利润的预报值是多少?
(ii)年宣传费 $\mathrm{x}$ 为何值时, 年利润的预报值最大?
附: 对于一组数据 $\left(u_{1} v_{1}\right),\left(u_{2} v_{2}\right) \ldots . .\left(u_{n} v_{n}\right)$, 其回归线 $v=\alpha+\beta u$ 的斜率和 截距的最小二乘估计分别为: $\widehat{\beta}=\frac{\sum_{i=1}^{n}\left(u_{i}-\bar{u}\right)\left(v_{i}-\bar{v}\right)}{\sum_{i=1}^{n}\left(u_{i}-\bar{u}\right)^{2}}, \widehat{\alpha}=\bar{v}-\widehat{\beta} u$.
在直角坐标系 $x O y$ 中, 曲线 $C: y=\frac{x^{2}}{4}$ 与直线 $\mathrm{I}: y=k x+a(a>0 )$ 交 于 $M, N$ 两点.
( I ) 当 $k=0$ 时, 分別求 $C$ 在点 $M$ 和 $N$ 处的切线方程.
(III) $y$ 轴上是否存在点 $\mathrm{P}$, 使得当 $\mathrm{k}$ 变动时, 总有 $\angle O P M=\angle O P N$ ? (说明理由 )
已知函数 $\mathrm{f}(\mathrm{x})=\mathrm{x}^{3}+\mathrm{ax}+\frac{1}{4}, \mathrm{~g}(\mathrm{x})=-\ln \mathrm{x}$
(i)当 $a$ 为何值时, $x$ 轴为曲线 $y=f(x)$ 的切线;
(ii)用 $\min \{\mathrm{m}, \mathrm{n}\}$ 表示 $\mathrm{m}, \mathrm{n}$ 中的最小值,设函数 $\mathrm{h}(\mathrm{x})=\min \{\mathrm{f}(\mathrm{x}), \mathrm{g}(\mathrm{x})$ \}$(\mathrm{x}>0)$, 讨论 $\mathrm{h}(\mathrm{x})$ 零点的个数.
选修 4 一 1:几何证明选讲
22. (10 分) 如图, $A B$ 是 $\odot O$ 的直径, $A C$ 是 $\odot O$ 的切线, $B C$ 交 $\odot O$ 于点 $E$.
( I ) 若 $D$ 为 $A C$ 的中点, 证明: $D E$ 是 $\odot O$ 的切线;
(II) 若 $\mathrm{OA}=\sqrt{3} \mathrm{CE}$, 求 $\angle A C B$ 的大小.
在直角坐标系 $x O y$ 中, 直线 $C_{1}: x=-2$, 圆 $C_{2}:(x-1)^{2}+(y-2$ )$^{2}=1$, 以坐标原点为极点, $x$ 轴的正半轴为极轴建立极坐标系.
( I ) 求 $C_{1}, C_{2}$ 的极坐标方程;
(II) 若直线 $C_{3}$ 的极坐标方程为 $\theta=\frac{\pi}{4}(\rho \in R)$, 设 $C_{2}$ 与 $C_{3}$ 的交点为 $M, N$, 求 $\triangle$ $\mathrm{C}_{2} \mathrm{MN}$ 的面积.
已知函数 $f(x)=|x+1|-2|x-a|, a>0$.
(I) 当 $a=1$ 时, 求不等式 $f(x)>1$ 的解集;
(II) 若 $f(x)$ 的图象与 $x$ 轴围成的三角形面积大于 6, 求 $a$ 的取值范围.