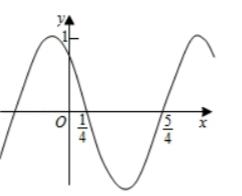
函数 $f(x)=\cos (\omega x+\phi)$ 的部分图象如图所示, 则 $f(x)$ 的单调递
减区间为
$\text{A.}$ $\left(k \pi-\frac{1}{4}, k \pi+\frac{3}{4}\right), k \in z$
$\text{B.}$ $\left(2 k \pi-\frac{1}{4}, 2 k \pi+\frac{3}{4}\right), k \in z$
$\text{C.}$ $\left(k-\frac{1}{4}, k+\frac{3}{4}\right), k \in z$
$\text{D.}$ $\left(2 k-\frac{1}{4}, 2 k+\frac{3}{4}\right), k \in z$