单选题 （共 10 题 ），每题只有一个选项正确
在下列简笔画图案中，是轴对称图形的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
关于 $x$ 的一元二次方程 $k x^2-2 k x+2=0$ 有两个相等的实数根，则 $k$ 的值是
$\text{A.}$ 0 或 2
$\text{B.}$ 2
$\text{C.}$ 0 或 -2
$\text{D.}$ -2
下列说法中，正确的是
$\text{A.}$ 对载人航天器零部件的检查适合采用抽样调查
$\text{B.}$ 某种彩票中奖的概率是 $\frac{1}{10}$ ，则购买 10 张这种彩票一定会中奖
$\text{C.}$ 为了了解一批洗衣粉的质量情况，从仓库中随机抽取 100 袋洗衣粉进行检验，这个问题中的 样本是 100
$\text{D.}$ 甲. 乙两人各进行了10次射击测试，他们的平均成绩相同，方差分别是 $s_{\text {甲 }}^2=3.2 ， s_{\mathrm{Z}}^2=1$ ， 则乙的射击成绩较稳定
一个长方形在平面直角坐标系中三个顶点的坐标为 $(-1,-1)$ ， $(-1,2) ，(3,-1)$ ，则第四个顶点的 坐标为
$\text{A.}$ $(2,2)$
$\text{B.}$ $(3,2)$
$\text{C.}$ $(3,3)$
$\text{D.}$ $(2,3)$
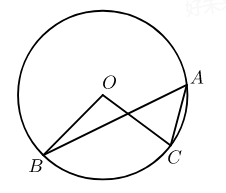
如图，点 $A ， B ， C$ 均在 $\odot O$ 上，且 $\angle B O C=90^{\circ}$ ，若 $\angle A C O$ 的度数为 $m^{\circ} ， \angle A B O$ 的度数为 $n^{\circ}$ ， 则 $m-n$ 的值是
$\text{A.}$ 30
$\text{B.}$ 45
$\text{C.}$ 50
$\text{D.}$ 60
已知二次函数 $y=2(x-3)^2-2$ ，下列说法: (1)其图象开口向上；(2)顶点坐标为 $(3,-2)$ ；(3)其图 象与 $y$ 轴的交点坐标为 $(0,-2)$ ；(4) 当 $x \leqslant 3$ 时， $y$ 随 $x$ 的增大而减小，其中正确的有
$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3个
$\text{D.}$ 4个
规定 $[x]$ 表示不大于 $x$ 的最大整数，例如 $[2.3]=2 ，[3]=3 ，[-2.5]=-3$. 那么函数 $y=[x]$ 的图象 为
$\text{A.}$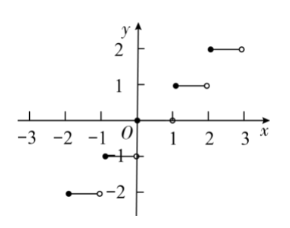 
$\text{B.}$ 
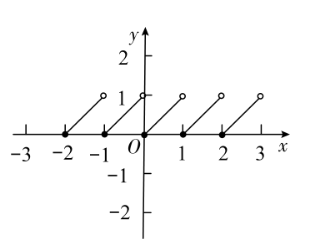$\text{C.}$ 
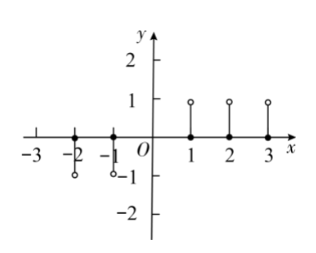$\text{D.}$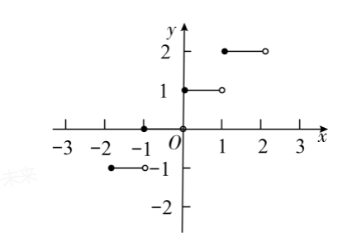 
如图， $D 、 E$ 分别是 $\triangle A B C$ 的边 $A B 、 B C$ 上的点，且 $D E / / A C$ ，若 $B E: E C=1: 3$ ，则 $\triangle D O E$ 与 $\triangle C O A$ 的周长之比为
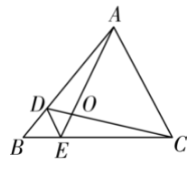
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{9}$
$\text{D.}$ $\frac{1}{16}$
某校园有一块正方形的空地，按如图所示划分区域种花，已知中间互相垂直的两条小路的宽分别 为 $1 \mathrm{~m}, 2 \mathrm{~m}$ ，且四个种花区域的面积相同，均为 $10 \mathrm{~m}^2$ ，设原正方形空地的边长为 $x \mathrm{~m}$ ，则下列方 程正确的是
$\text{A.}$ $x^2-3 x-40=0$
$\text{B.}$ $x^2-3 x-38=0$
$\text{C.}$ $x^2+3 x-40=0$
$\text{D.}$ $x^2+3 x-40=0$
已知抛物线 $y=a x^2+b x+c(a \neq 0)$ 如图所示，那么 $a 、 b 、 c$ 的取值范围是
$\text{A.}$ $a < 0, b>0, c>0$
$\text{B.}$ $a < 0, b < 0 、 c>0$
$\text{C.}$ $a < 0, b>0, c < 0$
$\text{D.}$ $a < 0, b < 0, c < 0$
填空题 （共 6 题 ），请把答案直接填写在答题纸上
在Rt $\triangle A B C$ 中， $\angle C=90^{\circ} ， A C=3 ， B C=4$ ，将 $\triangle A B C$ 绕边 $A C$ 所在直线旋转一周得到圆 锥，则该圆锥的侧面积是
若抛物线 $y=a x^2+c$ 与 $x$ 轴交于点 $A(m, 0), B(n, 0)$ ，与 $y$ 轴交于点 $C(0, c)$ ，则称 $\triangle A B C$ 为“抛物三 角形”，特别地，当 $m n c < 0$ 时，称 $\triangle A B C$ 为“正抛物三角形”；当 $m n c>0$ 时，称 $\triangle A B C$ 为“倒抛 物三角形"，那么，当 $\triangle A B C$ 为“倒抛物三角形"时， $a, c$ 应分别满足条件
若 $(m+1)^2+|n-2|=0$ ，则 $m^n=$
东方商厦将进货单价为 70 元的某种商品按零售价 100 元一个售出时，每天能卖出 20 个，若这种商 品的零售价在一定范围内每降价 1 元，其日销量就增加 1 个，为了获取最大利润，则应降 价 ________ 元.
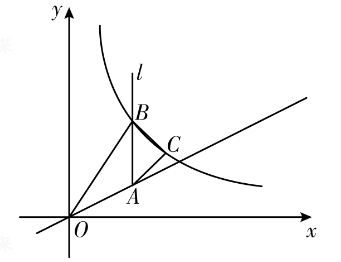
如图，已知点 $A$ 是一次函数 $y=\frac{1}{2} x(x \geqslant 0)$ 图象上一点，过点 $A$ 作 $x$ 轴的垂线 $l ， B$ 是 $l$ 上一点 $(B$ 在 $A$ 上方)，在 $A B$ 的右侧以 $A B$ 为斜边作等腰直角三角形 $A B C$ ，反比例函数 $y=\frac{k}{x}(x>0)$ 的图象过点 $B ， C$ ，若 $\triangle O A B$ 的面积为 6 ，则 $\triangle A B C$ 的面积是
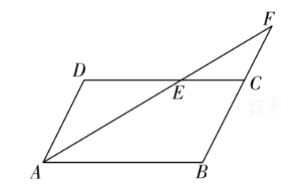
如图，在四边形 $A B C D$ 中， $A D=B C$ 且 $A D / / B C ， A B=5 ， A D=3 ， A E$ 平分 $\angle D A B$ 交 $B C$ 的延长线于 $F$ 点，则 $C F=$
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
回答下列问题：
（1）用配方法解方程: $x^2+4 x+1=0$.
（2）已知点 $(5,0)$ 在抛物线 $y=-x^2+(k+1) x-k$ 上. 求出抛物线的对称轴.
如图， $A B / / C D$ ，以点 $A$ 为圆心，小于 $A C$ 长为半径作圆弧，分别交 $A B ， A C$ 于 $E ， F$ 两点，再 分别以 $E ， F$ 为圆心，大于 $\frac{1}{2} E F$ 长为半径作圆弧，两条圆弧交于点 $P$ ，作射线 $A P ，$ 交 $C D$ 于点 $M$
（1）求证: $A P$ 平分 $\angle C A B$.
（2）若 $\angle A C D=114^{\circ}$ ，求 $\angle M A B$ 的度数.
手榴弹作为一种威力较大，体积较小，方便携带的武器，在战争中能发挥重要作用，然而想把手榴弹扔远，并不是一件容易的事．军训中，借助小山坡的有利地势，小刚在教官的指导下用模拟弹进行一次试投：如图所示，把小刚投出的手榴弹的运动路线看做一条抛物线，手榴弹飞行的最大高度为12米，此时它的水平飞行距离为6米，山坡OA的坡度为 1:3
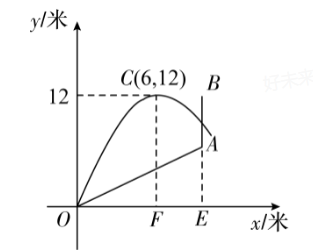
(1) 求这条抛物线的表达式;
（2）山坡上 $A$ 处的水平距离 $O E$ 为 9 米， $A$ 处有一棵树，树高 5 米，则小刚投出的手榴単能否越过 这棵树? 请说明理由;
(3) 求飞行的过程中手榴㫜离山坡的最大高度是多少米.
一只不透明袋子中装有 1 个白球和 2 个红球，这些球除颜色外都相同，某课外学习小组做莫球试 验: 将球搅匀后从中任意摸出 1 个球，记下颜色后放回、搅匀，不断重复这个过程.
（1）每一次摸到白球的概率为
（2）现从该袋中摸出 2 个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到 1 个白球， 1 个红球的概率.
如图，直线 $l$ 是一次函数 $y=k x+b$ 的图象，直线经过点 $(3,-3)$ ，交 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $B(0,1)$
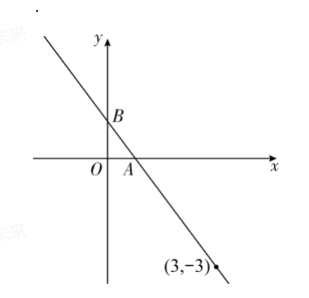
(1) 求直线 $l$ 的解析式.
(2) 求 $l$ 与两坐标轴所围成的三角形的面积.
（3）当 $x$ 时, $y \geqslant 0$.
（4）求原点到直线的距离.
已知: 如图， $\triangle A B C$ 是等边三角形， $A B=4 ， E$ 是 $B C$ 边上任意一点 (不与 $B 、 C$ 重合)，在 三角形外作等边 $\triangle C D E$ ，连接 $A E 、 B D$.
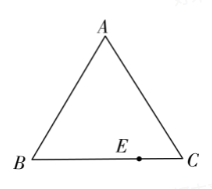
（1）根据题意画出图形.
（2）求证: $A E=B D$.
（3） $\triangle B D C$ 能否为直角三角形? 若能，求出 $B D$ 长；若不能，请说明理由.
在四边形 $A B C D$ 中， $A C$ 平分 $\angle D A B ， \angle A B C=\alpha ， \angle A D C=180^{\circ}-\alpha$.
(1) 若 $\alpha=90^{\circ}$ 时，直接写出 $C D$ 与 $C B$ 的数量关系为
(2) 如图 1 ，当 $\alpha \neq 90^{\circ}$ 时，（1）中结论是否还成立，说明理由.
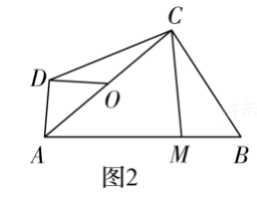
(3) 如图 $2 ， O$ 为 $A C$ 中点， $M$ 为 $A B$ 上一点， $B M=A D$ ，求 $\frac{C M}{D O}$ 的值.
如图，在平行四边形 $A B C D$ 中 $A D>A B$.
（1）尺规作图: 在 $A D$ 上截取 $A E$ ，使得 $A E=A B$. 作 $\angle A D C$ 的平分线交 $B C$ 于点 $F$ (保留作 图痕迹，不写作法）。
（2）在 (1) 所作图形中，连接 $B E$ ，求证：四边形 $B E D F$ 是平行四边形.（请补全下面的证 明过程，不写证明理由）.
证明: $\because D F$ 平分 $\angle A D C$ ，
$\therefore$ ________
$\because$ 在平行四边形 $A B C D$ 中， $B C / / A D$ ，
$\therefore$ ________
$$
\begin{aligned}
& \therefore \angle C D F=\angle C F D, \\
& \therefore C D=C F .
\end{aligned}
$$
$\because$ 在平行四边形 $A B C D$ 中， $A B=C D$ ，
$$
\begin{aligned}
& \text { 又 } \because A E=A B, \\
& \therefore A E=C F .
\end{aligned}
$$
$\because$ 在平行四边形 $A B C D$ 中， $A D=B C$ ，
$$
\therefore A D-A E=B C-C F \text {, }
$$
即 ________
又 ________
$\therefore$ 四边形 $B E D F$ 是平行四边形.
已知抛物线 $y=m x^2-(1-4 m) x+c$ 过点 $(1, a) ，(-1, a) ，(0,-1)$.
(1) 求该抛物线的解析式.
（2 ) 已知过原点的直线与该抛物线交于 $A ， B$ 两点（点 $A$ 在点 $B$ 右侧)，该抛物线的顶点为 $C$ ， 连接 $A C ， B C$ ，点 $D$ 在点 $A ， C$ 之间的抛物线上运动（不与点 $A ， C$ 重合) . 当点 $A$ 的横坐 标是 4 时，若 $\triangle A B C$ 的面积与 $\triangle A B D$ 的面积相等，求点 $D$ 的坐标.
（3）若直线与抛物线有且只有一个公共点，且与抛物线的对称轴不平行，则称该直线与抛物线 相切. 已知点 $F$ 的坐标是 $(0,1)$ ，过该抛物线上的任意一点 (除顶点外) 作该抛物线的切线 $l$ ，分别交直线 $y=1$ 和 $y=-3$ 直线于点 $P ， Q$ ，求 $F P^2-F Q^2$ 的值.