单选题 (共 12 题 ),每题只有一个选项正确
已知命题 $p: \forall x \geqslant 1, \ln x \geqslant \sqrt{x}+1$, 则 $\neg p$ 为
$\text{A.}$ $\exists x < 1, \ln x < \sqrt{x}+1$
$\text{B.}$ $\exists x \geqslant 1, \ln x < \sqrt{x}+1$
$\text{C.}$ $\exists x \geqslant 1, \ln x \geqslant \sqrt{x}+1$
$\text{D.}$ $\forall x < 1, \ln x < \sqrt{x}+1$
已知集合 $A=\{x \mid y=\ln (2-x)\}, B=\left\{x \mid x^2 < 9\right\}$, 则 $B \cap\left(\complement_{\mathbf{R}} A\right)=$
$\text{A.}$ $(-3,2]$
$\text{B.}$ $[-3,2)$
$\text{C.}$ $(2,3]$
$\text{D.}$ $[2,3)$
已知函数 $f(x)=\left\{\begin{array}{l}f(x+1)-f(x+2), x \leqslant 0, \\ x^2-4, x>0,\end{array} g(x)=\log _a x(a>0\right.$ 且 $a \neq 1)$, 若 $f(0)=g(8)$, 则 $a=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
我们知道, 人们对声音有不同的感觉, 这与声音的强度有关系. 声音的强度常用 $I$ (单位: 瓦 $/$ 米 ${ }^2$, 即 $\mathrm{W} / \mathrm{m}^2$ ) 表示, 但在实际测量时, 声音的强度水平常用 $L$ (单位: 分贝) 表示, 它们满足换算公式: $L=10 \lg \frac{I}{I_0}(L \geqslant 0$, 其中 $I_0=1 \times 10^{-12} \mathrm{~W} / \mathrm{m}^2$ 是人们能听到的最小声音的强度, 是听觉的开端). 若使某小区内公共场所声 音的强度水平降低 10 分贝 , 则声音的强度应变为原来的
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{1}{100}$
$\text{C.}$ $\frac{1}{10}$
$\text{D.}$ $\frac{1}{20}$
“ $\ln a < \ln b$ ”是“ $a^{\frac{1}{3}} < b^{\frac{1}{3}}$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知函数 $f(x)=a x^3+b x+3(a, b \in \mathbf{R})$. 若 $f(2)=5$, 则 $f(-2)=$
$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 1
已知函数 $f(x)=\frac{d}{a x^2+b x+c}(a, b, c, d \in \mathbf{R})$ 的图象如图所示, 则下列判断 正确的是
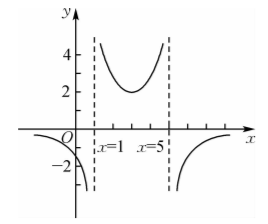
$\text{A.}$ $a>0, b>0, c < 0, d>0$
$\text{B.}$ $a < 0, b>0, c < 0, d>0$
$\text{C.}$ $a < 0, b>0, c>0, d>0$
$\text{D.}$ $a>0, b < 0, c>0, d>0$
若偶函数 $f(x)$ 在 $(-\infty, 0]$ 上单调递减, $a=f\left(\log _2 3\right), b=f\left(\log _4 5\right), c=f\left(2^{\frac{3}{2}}\right)$, 则 $a, b, c$ 满足
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < a < c$
$\text{C.}$ $c < a < b$
$\text{D.}$ $c < b < a$
已知函数 $f(x)$ 满足: 当 $x \leqslant a$ 时, $f(x)=x^3-x$, 且 $f(a+x)=f(a-x)$. 若函数 $f(x)$ 恰有 5 个零点, 则 $a=$
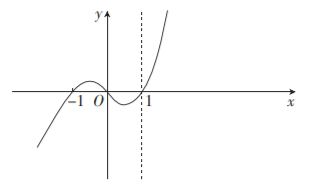
$\text{A.}$ $-2$
$\text{B.}$ $-1$
$\text{C.}$ $0$
$\text{D.}$ $1$
已知函数 $f(x)=\mathrm{e}^{4 x-1}, g(x)=\frac{1}{2}+\ln 2 x$, 若 $f(m)=g(n)$ 成立, 则 $n-m$ 的最小值为
$\text{A.}$ $\frac{1-\ln 2}{4}$
$\text{B.}$ $\frac{2 \ln 2-1}{3}$
$\text{C.}$ $\frac{1+\ln 2}{4}$
$\text{D.}$ $\frac{1+2 \ln 2}{3}$
已知定义在 $\mathbf{R}$ 上的连续奇函数 $f(x)$ 的导函数为 $f^{\prime}(x)$, 当 $x>0$ 时, $f^{\prime}(x)+\frac{f(x)}{x}>0$, 则使得 $2 x f(2 x)+(1-3 x) f(3 x-1)>0$ 成立的 $x$ 的取值范围是
$\text{A.}$ $\left(\frac{1}{5}, 1\right)$
$\text{B.}$ $\left(-1, \frac{1}{5}\right) \cup(1,+\infty)$
$\text{C.}$ $(1,+\infty)$
$\text{D.}$ $(-\infty, 1)$
定义 “函数 $y=f(x)$ 是 $D$ 上的 $a$ 级类周期函数”如下: 函数 $y=f(x), x \in D$, 对于给定的非零常数 $a$, 总存在非零常数 $T$, 使得定义域 $D$ 内的任意实数 $x$ 都有 $a f(x)=f(x+T)$ 恒成立, 此时 $T$ 为 $f(x)$ 的 周期. 若 $y=f(x)$ 是 $[1,+\infty)$ 上的 $a$ 级类周期函数, 且 $T=1$, 当 $x \in[1,2)$ 时, $f(x)=2^x(2 x+1)$, 且 $y=f(x)$ 是 $[1,+\infty)$ 上的单调递增函数, 则实数 $a$ 的取值范围为
$\text{A.}$ $\left[\frac{5}{6},+\infty\right)$
$\text{B.}$ $[2,+\infty)$
$\text{C.}$ $\left[\frac{10}{3},+\infty\right)$
$\text{D.}$ $[10,+\infty)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)=(x+1)(x+a) x^4$ 为 $\mathbf{R}$ 上的偶函数, 则 $a=$
若函数 $y=2 x^3+1$ 与 $y=3 x^2-b$ 的图象在一个公共点处的切线相同, 则实数 $b=$
函数 $f(x)=\frac{\ln x}{x}-x$ 在区间 $(0, \mathrm{e}]$ 上的最大值是
设函数 $f(x)=\frac{1}{3} x^3-\frac{1}{2}(a+1) x^2+a x$, 集合 $M=\{x \mid f(x) < 0\}, P=\left\{x \mid f^{\prime}(x) < 0\right\}$, 若 $P \subsetneqq M$, 则实数$a$ 的取值构成的集合是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设函数 $f(x)=\sqrt{4^x-32}$ 的定义域为集合 $A$, 集合 $B=\left\{x \mid x^2+a x-6 < 0\right\}$.
(1)若 $a=-5$, 求 $A \cap B$;
(2)若 $3 \notin B$, 且 $-2 \notin B$, 求 $\left(\complement_{\mathbf{R}} A\right) \bigcap\left(\complement_{\mathbf{R}} B\right)$.
已知函数 $f(x)=x^2+b x-1$ 有两个零点 $x_1, x_2$, 且 $x_1, x_2$ 的倒数和为 $-1$.
(1) 求函数 $f(x)$ 的解析式;
(2) 若在区间 $[-2,1]$ 上, 不等式 $f(-x)>2 x-m$ 恒成立, 求实数 $m$ 的取值范围.
已知 $p$ : 函数 $y=\ln \left(m x^2-4 x+m\right)$ 的定义域为 $\mathbf{R}, q$ : 存在 $x \in\left[0, \frac{1}{2}\right]$, 使得不等式 $x^2-x+m-\frac{5}{4} \geqslant 0$ 成立.
(1) 若 $p$ 为真, 求实数 $m$ 的取值范围;
(2) 若 $(\neg p) \vee q$ 为真且 $(\neg p) \wedge q$ 为假, 求实数 $m$ 的取值范围.
已知函数 $f(x)=\log _{\frac{1}{2}} \frac{2-a x}{x-2}(a \in \mathbf{R})$ 的图象关于原点对称.
(1) 当 $x \in(2,+\infty)$ 时, $f(x)+\log _{\frac{1}{2}}(x-2) < m$ 恒成立, 求实数 $m$ 的取值范围;
(2) 若关于 $x$ 的方程 $f(x)=\log _{\frac{1}{2}}(x+k)$ 在 $(2,5]$ 上有解, 求实数 $k$ 的取值范围.
已知函数 $f(x)=\frac{1}{2} x^2, g(x)=\mathrm{eln} x$.
(1) 设函数 $F(x)=f(x)-g(x)$, 求 $F(x)$ 的单调区间;
(2) 若存在常数 $k, m$, 使得 $f(x) \geqslant k x+m$, 对 $x \in \mathbf{R}$ 恒成立, 且 $g(x) \leqslant k x+m$, 对 $x \in(0,+\infty)$ 恒成立, 则称直线 $y=k x+m$ 为函数 $f(x)$ 与 $g(x)$ 的 “分界线”, 试问: $f(x)$ 与 $g(x)$ 是否存在“分界线”? 若 存在,求出“分界线”的方程; 若不存在, 请说明理由.
已知函数 $f(x)=a \mathrm{e}^x-x+1(a \in \mathbf{R})$.
(1) 讨论函数 $f(x)$ 的零点的个数;
(2) 若 $f(x)$ 有两个不同的零点 $x_1 、 x_2$, 证明: $x_1+x_2>4$.