单选题 (共 10 题 ),每题只有一个选项正确
一元二次方程 $(x+3)(2 x-1)=0$ 的解是
$\text{A.}$ $x_1=3, x_2=\frac{1}{2}$
$\text{B.}$ $x_1=-3, x_2=\frac{1}{2}$
$\text{C.}$ $x_1=3, x_2=2$
$\text{D.}$ $x_1=-3, x_2=-2$
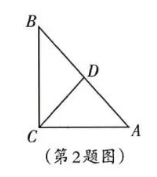
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, C D$ 是 $\triangle A B C$ 的中线, $A C=8, A B=12$, 则 $C D$ 的长等于
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 8
$\text{D.}$ 6
一元二次方程 $x^2-2 x-1=0$ 根的情况是
$\text{A.}$ 有两个不相等的实数根
$\text{B.}$ 有两个相等的实数根
$\text{C.}$ 没有实数根
$\text{D.}$ 只有一个实数根
在一个不透明的口袋中有红色、黄色和绿色球共 60 个, 它们除颜色外, 其余完全相同. 在不 倒出球的情况下, 要估计袋中各种颜色球的个数. 同学们通过大量的摸球试验后, 发现摸 到红球、黄球和绿球的频率分别稳定在 $20 \%, 40 \%$ 和 $40 \%$. 由此, 推测口袋中黄色球的个数有
$\text{A.}$ 15 个
$\text{B.}$ 20 个
$\text{C.}$ 21 个
$\text{D.}$ 24 个
小亮仿照探究一元二次方程解的方法,课后尝试探究了一元三次方程 $x^3+12 x^2-15 x-1=0$ 的解,列表如下:

据此可知, 方程 $x^3+12 x^2-15 x-1=0$ 的一个解 $x$ 的取值范围是
$\text{A.}$ $0 < x < 0.5$
$\text{B.}$ $0.5 < x < 1$
$\text{C.}$ $1 < x < 1.5$
$\text{D.}$ $1.5 < x < 2$
在复习特殊的平行四边形时, 某小组同学画出了如下关系图, 组内一名同学在箭头处填写 了它们之间转换的条件, 其中填写错误的是
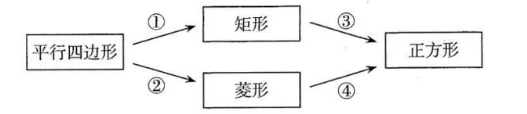
$\text{A.}$ (1), 对角相等
$\text{B.}$ (3), 有一组邻边相等
$\text{C.}$ (2), 对角线互相垂直
$\text{D.}$ (4), 有一个角是直角
今年全球多地持续高温天气, 我国的煤碳进口量也大幅增加. 据海关总署发布的数据显 示, 2022 年 8 月份我国进口煤炭约 2952 万吨, 而 2020 年 8 月份我国进口煤炭约 2056 万吨. 设这三年每年 8 月份我国进口煤碳的平均增长率为 $x$, 则根据题意列出的方程是
$\text{A.}$ $2056(1+2 x)^2=2952$
$\text{B.}$ $2056(1+x)^2=2952$
$\text{C.}$ $2952(1-x)^2=2056$
$\text{D.}$ $2056(1+x)+2056(1+x)^2=2952$
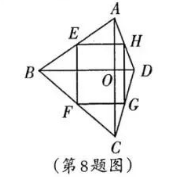
如图, 四边形 $A B C D$ 的对角线 $A C \perp B D$ 于点 $O$, 点 $E, F, G, H$ 分别为边 $A B$, $B C, C D$ 和 $A D$ 的中点, 顺次连接 $E F, F G, G H$ 和 $H E$ 得到四边形 $E F G H$. 若 $A C=10, B D=8$, 则四边形 $E F G H$ 的面积等于
$\text{A.}$ 45
$\text{B.}$ 40
$\text{C.}$ 20
$\text{D.}$ 18
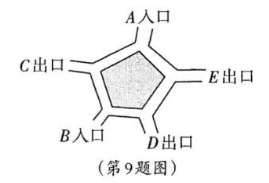
我市举办的“喜迎二十大 奋进新征程”吸引了众多市民前来参观,如图是该展览馆出人口示意图. 小颖和母亲从同一人口进人分别参观, 参观结束后, 她们恰好从同一出口走出的概率是
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{6}$
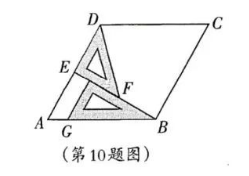
如图, 在菱形 $A B C D$ 中摆放了一副三角板. 等腰直角三角板 $D E F$ 的一条直角边 $D E$ 在菱形边 $A D$ 上, 直角顶点 $E$ 为 $A D$ 的中点, 含 $30^{\circ}$ 角的直角三角板的斜边 $G B$ 在菱形 $A B C D$ 的边 $A B$ 上. $\angle C D F$ 的度数等于
$\text{A.}$ $55^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $75^{\circ}$
$\text{D.}$ $85^{\circ}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
已知关于 $x$ 的方程 $x^2+k x+3=0$ 的一个根是 1 , 则实数 $k$ 等于
现在进行配紫色游戏: 同时转动如图所示的 $\mathrm{A}$ 和 $\mathrm{B}$ 两个转盘, 若 一个指针指向红色, 另一个指针指向蓝色时就配成紫色; 若指针 指在分界线上时, 就需要重新转动转盘. 转动一次配成紫色的 概率为

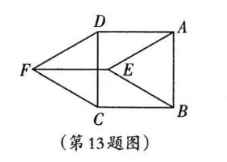
如图,点 $E, F$ 分别是正方形 $A B C D$ 内部、外部一点, 四边形 $A D F E$ 与四边形 $B C F E$ 均为菱形, 则 $\angle C B E$ 的度数等于
一个小球从地面坚直向上弹出, 它在空中距离地面的高度 $h(\mathrm{~m})$ 与弹出的时间 $t(\mathrm{~s})$ 满足的关系式为 $h=15 t-5 t^2$. 当小球第一次距 离地面 $10 \mathrm{~m}$ 时, 小球弹出的时间为 秒.
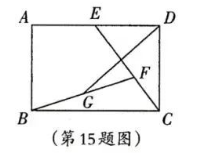
如图, 在矩形 $A B C D$ 中, $A D=6$, 点 $E$ 为 $A D$ 的中点, 连接 $C E$. 点 $F$ 是 $C E$ 上的动点, 点 $G$ 为 $B F$ 的中点, 连接 $D G$.
从 $\mathbf{A}, \mathbf{B}$ 两题中任选一题作答.
A. 当 $A B=3$ 时, $D G$ 的最小值是
B. 当 $A B=4$ 时, $D G$ 的最小值是
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解方程:
(1) $x^2-6 x-3=0$;
(2) $2 x^2+5 x+1=0$.
如图, 把两个正方形 $A B C D$ 和 $C E F G$ 拼成如图所示的图案, 点 $B, C, E$ 在同一直线上, 连接 $A C, C F$. 求 $\angle A C F$ 的度数.

直角三角形中 “勾三股四弦五”这一特殊关系, 在中国称为 “商高定理”, 在国外又称为 “毕 达哥拉斯定理”. 由此发现三个连续正整数 $3,4,5$, 满足 $3^2+4^2=5^2$, 即前两个数的平方和等 于第三个数的平方. 请你探究: 是否存在五个连续正整数, 满足前三个数的平方和等于后 两个数的平方和? 若存在, 请求出这五个正整数; 若不存在, 请说明理由.
如图, 菱形 $A B C D$ 的对角线 $A C$ 和 $B D$ 相交于点 $O$, 过点 $D$ 作 $A C$ 的平行线并在其上截取 $D E=\frac{1}{2} A C$, 连接 $C E$.
求证: 四边形 $O C E D$ 是矩形.

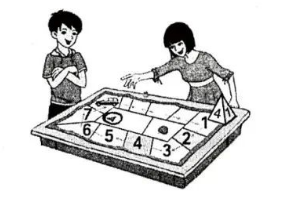
如图, 有一个质地均匀且四个面上分别标有数字 $1,2,3,4$ 的正四面体骰子, 小明与小红按 照以下规则进行游戏活动: 两人轮流郑这枚骰子, 骰子朝下的数字是几, 就将骰子前进几 格. 开始骰子在数字“1”的那一格, 小明先郑骰子. 请解答下列问题:
(1) 小明郑出骰子, 数字 3 朝下的概率是
(2)求小红第一次郑完骰子后, 骰子前进到数字“7”那一 格的概率(用列表或画树状图的方法进行解答).
在矩形 $A B C D$ 中, $\angle D A B$ 的角平分线 $A E$ 交边 $C D$ 于点 $E$.
(1) 如图 1, $\angle A B C$ 的角平分线 $B F$ 交边 $C D$ 于点 $F$, 求证: $D F=C E$;
(2) 如图 2, 当点 $E$ 与点 $C$ 重合时.
(1) 作 $\angle A B C$ 的角平分线 $B G$ 交 $A C$ 于点 $O$;
(2)当 $A B=4$ 时,求(1)中 $B O$ 的长.

某灯具制造厂新研发出一种节能护眼台灯, 该台灯的成本价为 30 元/盛. 试销一段时间 后, 发现按 40 元/盛的价格销售, 每周可售出 600 盙; 当每盙台灯售价在 40 元至 60 元之间 时,每盙售价每上涨 2 元,每周的销售量将减少 20 盙.
(1)若每盛台灯销售价为 46 元,求这周的销售利润;
(2)如果要实现每周的销售利润 10000 元的目标,求每盎台灯的销售价格.
操作与探究
操作: 在数学实践课上, 老师要求同学们对如图 1 的 $\triangle A B C$ 纸片进行以下操作, 并探究其 中的问题:

第一步: 如图 2, 沿过点 $B$ 的直线折叠, 使得点 $A$ 落在 $B C$ 上, 展开铺平该纸片, 折痕为 $B D$;
第二步: 如图 3, 继续折叠该纸片, 使得点 $B$ 与点 $D$ 重合, 展开铺平该纸片, 折痕为 $E F$;
第三步: 如图 4, 连接 $D E, D F$.
探究一:判断四边形 $B E D F$ 的形状, 并说明理由;
探究二: 在 $\triangle A B C$ 纸片中, $\angle A=105^{\circ}, \angle A B C=30^{\circ}, B C=6+2 \sqrt{3}$. 从 $\mathbf{A}, \mathbf{B}$ 两题中任选一题作答.
A. 求四边形 $B E D F$ 的面积.
B. 设点 $P$ 在 $B D$ 上运动, 连接 $C P, P F$, 求 $C P+P F$ 的最小值.
