单选题 (共 10 题 ),每题只有一个选项正确
在 $\frac{1}{2}, 0,-1,-\sqrt{2}$ 这四个数中, 最小的数是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $0$
$\text{C.}$ $-1$
$\text{D.}$ $-\sqrt{2}$
2022 年 3 月, 国务院总理李克强在政府工作报告中指出: 2021 年, 我国经济保持恢复发展, 国内生产总值达到 1140000 亿元. 将 1140000 用科学记数法表示应为
$\text{A.}$ $0.114 \times 10^7$
$\text{B.}$ $1.14 \times 10^7$
$\text{C.}$ $1.14 \times 10^6$
$\text{D.}$ $11.4 \times 10^5$
下列计算正确的是
$\text{A.}$ $2 x+3 y=5 x y$
$\text{B.}$ $\left(a b^2\right)^2=a b^4$
$\text{C.}$ $(a+b)^2=a^2+b^2$
$\text{D.}$ $5 m^2 \cdot m^3=5 m^5$
共同富裕的要求是: 在消除两极分化和贫穷基础上实现普遍富裕.下列有关个人收入的统计量中, 最能体现共同富裕要求的是
$\text{A.}$ 平均数小, 方差大
$\text{B.}$ 平均数小, 方差小
$\text{C.}$ 平均数大, 方差小
$\text{D.}$ 平均数大, 方差大
化简 $\frac{x^2}{x-1}+\frac{1}{1-x}$ 的结果是
$\text{A.}$ $x+1$
$\text{B.}$ $\frac{1}{x+1}$
$\text{C.}$ $x-1$
$\text{D.}$ $\frac{x}{x-1}$
《九章算术》中有问题: 把一份文件送到 900 里外的城市, 如果用慢马送, 需要的时间比规 定时间多一天:如果用快马送, 所需的时间比规定时间少 3 天. 已知快马的速度是慢马的 2 倍, 求规定时间. 设规定时间为 $x$ 天, 则可列方程为
$\text{A.}$ $\frac{900}{x+1}=\frac{900}{x-3} \times 2$
$\text{B.}$ $\frac{900}{x+1} \times 2=\frac{900}{x-3}$
$\text{C.}$ $\frac{900}{x-1}=\frac{900}{x+3} \times 2$
$\text{D.}$ $\frac{900}{x-1} \times 2=\frac{900}{x+3}$
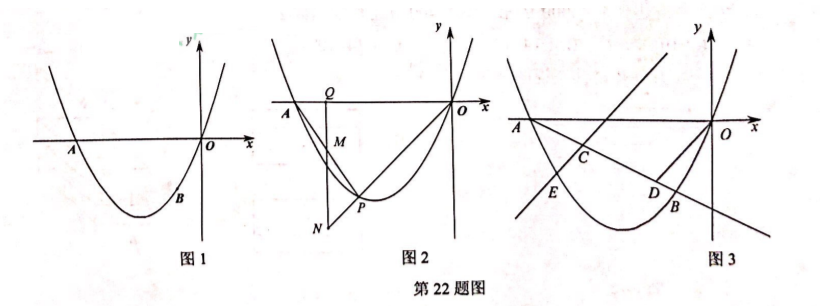
某学校安装红外线体温检测仪 (如图 1), 其红外线探测点 $O$ 可以在垂直于地面的支杆 $O P$ 上自由调节 (如图 2). 已知最大探测角 $\angle O B C=67^{\circ}$, 最小探测角 $\angle O A C=37^{\circ}$. 测温区域 $A B$ 的长度为 2 米, 则该设备的安装高度 $O C$ 应调整为 $(\quad)$ 米. (精确到 $0.1$ 米.
参考数据: $\sin 67^{\circ} \approx \frac{12}{13}, \cos 67^{\circ} \approx \frac{5}{13}, \tan 67^{\circ} \approx \frac{12}{5}, \sin 37^{\circ} \approx \frac{3}{5}, \cos 37^{\circ} \approx \frac{4}{5}, \tan 37^{\circ} \approx \frac{3}{4}$ )
$\text{A.}$ $2.4$
$\text{B.}$ $2.2$
$\text{C.}$ $3.0$
$\text{D.}$ $2.7$
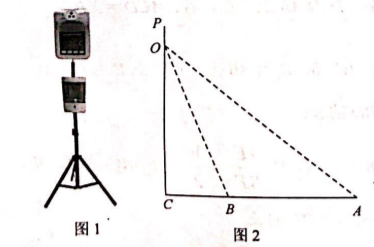
二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图象的一部分如图所示. 已知图象经过点 $(-1,0)$, 其 对称轴为直线 $x=1$. 下列结论:
①$a b c < 0$;
②$4 a+2 b+c < 0$;
③$8 a+c < 0$;
④若抛物线经过 点 $(-3, n)$, 则关于 $x$ 的一元二次方程 $a x^2+b x+c-n=0(a \neq 0)$ 的两根分别为 $-3,5$.
上 述结论中正确结论的个数为
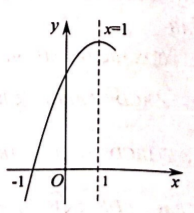
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
如图, 在正方形 $A B C D$ 中, 点 $G$ 是 $B C$ 上一点, 且 $\frac{G C}{B G}=\frac{1}{2}$, 连接 $D G$ 交对角线 $A C$ 于 $F$ 点, 过 $D$ 点作 $D E \perp D G$ 交 $C A$ 的延长线于点 $E$, 若 $A E=3$, 则 $D F$ 的长为
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $\frac{4 \sqrt{5}}{3}$
$\text{C.}$ $\frac{9}{2}$
$\text{D.}$ $\frac{3 \sqrt{5}}{2}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
一个不透明的袋子中装有除颜色外其它均相同的 4 个白球和若干个绿球, 每次摇均匀后随 机摸出一个球, 记下颜色后再放回袋中, 经大量试验, 发现摸到绿球的频率稳定在 $0.6$, 则 绿球的个数为
上海举办过第十四届国际数学教育大会 (简称 ICME-14). 会徽的主题图案 (如图) 有着丰富 的数学元素, 展现了中国古代数学的灲烂文明, 图案中右下方的图形是用中国古代的计数符 号写出的八进制数字 3745 . 我们常用的数是十进制数, 如 $4657=4 \times 10^3+6 \times 10^2+5 \times 10^1+7 \times 10^0$, 在电子计算机中用的二进制, 如二进制中 $110=1 \times 2^2+1 \times 2^1+0 \times 2^0$ 等于十进制的数 6 , 八进制 数字 3745 换算成十进制是

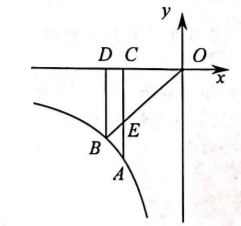
如图, 点 $A$ 是反比例函数 $y=\frac{\kappa}{x}$ 的图象的第三象限上一点, $A C \perp x$ 轴, 垂足为点 $C, E$ 为 $A C$ 上一点, 且 $\frac{A E}{C E}=\frac{2}{3}$, 连接 $O E$ 并延长交 $y=\frac{k}{x}$ 的图象的第三象限上另一点 $B$, 过 $B$ 点 作 $B D \perp x$ 轴, 垂足为点 $D$, 四边形 $B E C D$ 的面积为 2 , 则 $k$ 的值是
如图, 已知 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, D$ 为 $A B$ 的中点, $A E \perp C D$ 于 $F$, 交 $B C$ 于 $E$, 连接 $B F$, 若 $\angle B F E=45^{\circ}$, 则 $\frac{C E}{B E}$ 的值为

解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(\sqrt{2022}-\pi)^0+2^{-2}-2 \cos 45^{\circ}+|1-\sqrt{2}|$.
如图是由边长为 1 的小正方形构成的 $6 \times 6$ 的网格, 点 $A, B$ 均在格点上 (图中小正 方形的顶点称为格点).
(1) 在图 1 的网格内画出以 $A B$ 为对角线的正方形 $A C B D$, 点 $C, D$ 为格点;
(2) 在图 2 的网格内画出以 $A B$ 为边且周长最大的 $\square A B C D$, 点 $C, D$ 为格点(画一个即可).

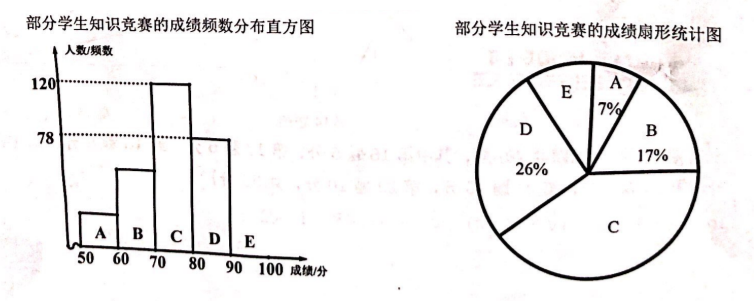
某初中学校组织了全校学生参加 “珍惜生命, 远离新冠病毒” 的知识竞赛, 从中 抽取了部分学生的成绩, 分为 5 组: $A$ 组 $50 \sim 60 ; B$ 组 60 70; $C$ 组 70 80; D 组 80 90; $E$ 组 90 100 (每组含最小值不含最大值), 统计后得到如图所示的频数分布直方图和扇形 统计图.
(1) 抽取学生的总人数是 ( ) 人, 扇形 $C$ 的圆心角是 ( ) 度;
(2) 补全频数分布直方图;
(3) 该校共有 2200 名学生, 若成绩在 70 分以下 (不含 70 分) 的学生防疫意识不强, 有待进 一步加强, 则该校防疫意识不强的学生约有多少人?
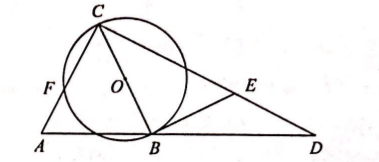
如图, 在 $\triangle A B C$ 中, $A C=B C$, 以 $B C$ 为 直径作 $\odot O$, 交 $A C$ 于点 $F$, 过 $C$ 点作 $C D \perp$ $A C$ 交 $A B$ 延长线于点 $D, E$ 为 $C D$ 上一点, 且 $E B=E D$.
(1) 求证: $B E$ 为 $\odot O$ 的切线:
(2) 若 $A F=2, \tan A=2$, 求 $B E$ 的长.
草莓基地对收获的草莓分拣成 $\mathrm{A}, \mathrm{B}$ 两个等级销售, 每千克草莓的价格 $\mathrm{A}$ 级比 $\mathrm{B}$
(1) 问草莓基地销售 $A, B$ 两个等级草莓每千克各是多少元?
(2) 某超市从该草莓基地购进 200 千克草莓, A 级草莓不少于 40 千克, 且总费用不超过 3800 元, 超市对购进的草苺进行包装销售 (如下表), 全部包装销售完, 当包装 A 级草苺多少 包时, 所获总利润最大? 最大总利润为多少元?

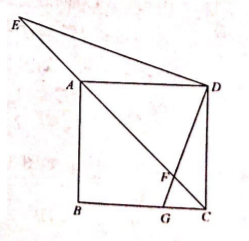
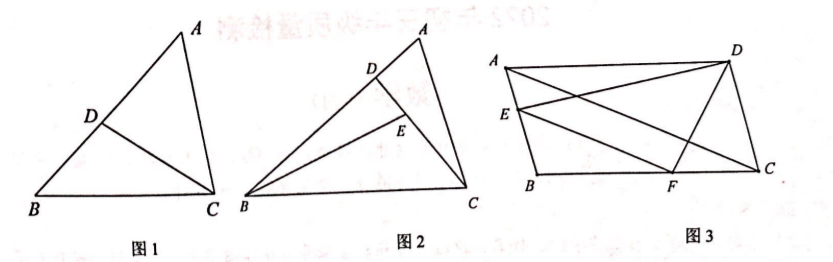
(1) 问题背景: 如图 1, 在 $\triangle A B C$ 中, $D$ 为 $A B$ 上一点, 若 $\angle A C D=\angle B$. 求证: $A C^2=A D \cdot A B$;
(2) 尝试应用: 如图 2, 在 $\triangle A B C$ 中, $A B=9, A C=6, D$ 为 $A B$ 上一点, 点 $E$ 为 $C D$ 上一 点, 且 $\frac{D E}{E C}=\frac{1}{2}, \angle A C D=\angle A B E$, 求 $B D$ 的长;
(3) 拓展创新: 如图 3, $\square A B C D$ 中, $E$ 是 $A B$ 上一点, 且 $\frac{A E}{B E}=\frac{1}{2}, E F / / A C$, 连接 $D E$, $D F$, 若 $\angle E D F=\angle B A C, D F=5 \sqrt{6}$, 直接写出 $A B$ 的长.
如图 1, 抛物线 $y=a x^2+b x$ 经过点 $A(-5,0)$, 点 $B(-1,-2)$.
(1) 求抛物线解析式;
(2) 如图 2, 点 $P$ 为抛物线上第三象限内一动点, 过点 $Q(-4,0)$ 作 $y$ 轴的平行线, 交直线 $A P$ 于点 $M$, 交直线 $O P$ 于点 $N$, 当点 $P$ 运动时, $4 Q M+Q N$ 的值是否变化? 若变化, 说明变化 规律, 若不变, 求其值;
(3) 如图 3, 长度为 $\sqrt{5}$ 的线段 $C D$ (点 $C$ 在点 $D$ 的左边) 在射线 $A B$ 上移动 (点 $C$ 在线段 $A B$ 上), 连接 $O D$, 过点 $C$ 作 $C E / / O D$ 交抛物线于点 $E$, 线段 $C D$ 在移动的过程中, 直线 $C E$ 经过一定点 $F$, 直接写出定点 $F$ 的坐标与 $\frac{F C}{E C}$ 的最小值.