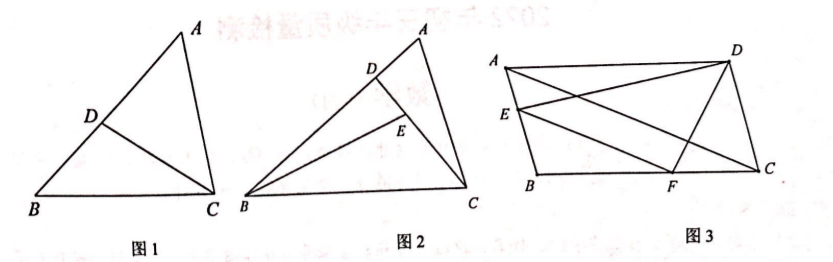
(1) 问题背景: 如图 1, 在 $\triangle A B C$ 中, $D$ 为 $A B$ 上一点, 若 $\angle A C D=\angle B$. 求证: $A C^2=A D \cdot A B$;
(2) 尝试应用: 如图 2, 在 $\triangle A B C$ 中, $A B=9, A C=6, D$ 为 $A B$ 上一点, 点 $E$ 为 $C D$ 上一 点, 且 $\frac{D E}{E C}=\frac{1}{2}, \angle A C D=\angle A B E$, 求 $B D$ 的长;
(3) 拓展创新: 如图 3, $\square A B C D$ 中, $E$ 是 $A B$ 上一点, 且 $\frac{A E}{B E}=\frac{1}{2}, E F / / A C$, 连接 $D E$, $D F$, 若 $\angle E D F=\angle B A C, D F=5 \sqrt{6}$, 直接写出 $A B$ 的长.