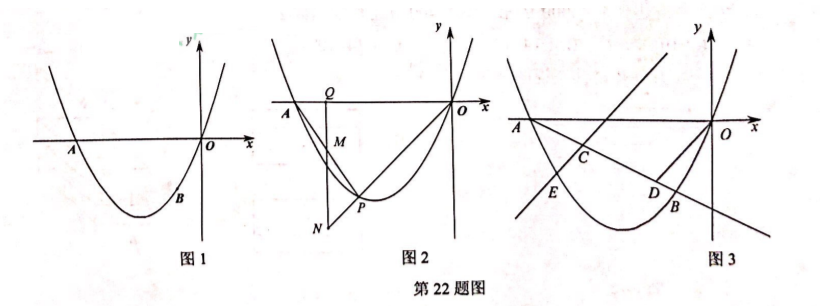
如图 1, 抛物线 $y=a x^2+b x$ 经过点 $A(-5,0)$, 点 $B(-1,-2)$.
(1) 求抛物线解析式;
(2) 如图 2, 点 $P$ 为抛物线上第三象限内一动点, 过点 $Q(-4,0)$ 作 $y$ 轴的平行线, 交直线 $A P$ 于点 $M$, 交直线 $O P$ 于点 $N$, 当点 $P$ 运动时, $4 Q M+Q N$ 的值是否变化? 若变化, 说明变化 规律, 若不变, 求其值;
(3) 如图 3, 长度为 $\sqrt{5}$ 的线段 $C D$ (点 $C$ 在点 $D$ 的左边) 在射线 $A B$ 上移动 (点 $C$ 在线段 $A B$ 上), 连接 $O D$, 过点 $C$ 作 $C E / / O D$ 交抛物线于点 $E$, 线段 $C D$ 在移动的过程中, 直线 $C E$ 经过一定点 $F$, 直接写出定点 $F$ 的坐标与 $\frac{F C}{E C}$ 的最小值.