单选题 （共 10 题 ），每题只有一个选项正确
已知关于 $x$ 的 $-$ 元二次方程 $2 x^2-x+m^2-9=0$ 有一个根是 0 , 则 $m$ 的值为 ( )
$\text{A.}$ $3$
$\text{B.}$ $3$ 或$-3$
$\text{C.}$ $-3$
$\text{D.}$ 不等于 $3$ 的任意实数
二次函数 $y=3(x+5)^2+4$ 图像的顶点坐标是
$\text{A.}$ $(5,4)$
$\text{B.}$ $(-5,4)$
$\text{C.}$ $(5,-4)$
$\text{D.}$ 无法确定
方程 $x^2-9 x+18=0$ 的两个根是等膤三角形的底和腰, 则这个三角形的周长为
$\text{A.}$ 12
$\text{B.}$ 15
$\text{C.}$ 12 或 15
$\text{D.}$ 不能确定
将抛物线 $y=3 x^2$ 先向左平移 2 个单位, 再向下平移 1 个单位, 得到新抛物线的解析式是
$\text{A.}$ $y=3(x+2)^2-1$
$\text{B.}$ $y=3(x+2)^2+1$
$\text{C.}$ $y=3(x-2)^2-1$
$\text{D.}$ $y=3(x-2)^2+1$
某机械厂七月份生产零件 50 万个, 第三季度生产零件 196 万个. 设该厂八、九月份 平均每月的增长率为 $x$, 那么 $x$ 满足的方程是
$\text{A.}$ $50\left(1+x^2\right)=196$
$\text{B.}$ $50+50\left(1+x^2\right)=196$
$\text{C.}$ $50+50(1+x)+50(1+x)^2=196$
$\text{D.}$ $50+50(1+x)+50(1+2 x)=196$
已知关于 $x$ 的一元二次方程 $(k-1) x^2+2 x-2=0$ 有实数㮩, 则 $k$ 的取值范围是
$\text{A.}$ $k>\frac{1}{2}$
$\text{B.}$ $k \geq \frac{1}{2}$
$\text{C.}$ $k>\frac{1}{2}$ 且 $k \neq 1$
$\text{D.}$ $k \geq \frac{1}{2}$ 且 $k \neq 1$
设 $a, b$ 是方程 $x^2+x-2022=0$ 的两个实数根, 则 $a^2+2 a+b$ 的值为
$\text{A.}$ 2020
$\text{B.}$ 2021
$\text{C.}$ 2022
$\text{D.}$ 2023
在同一坐标系内, 一次函数 $y=a x+b$ 与二次函数 $y=a x^2+8 x+b$ 的图像可能是
$\text{A.}$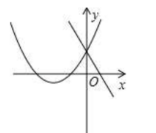 
$\text{B.}$ 
$\text{C.}$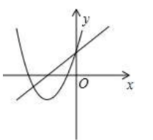 
$\text{D.}$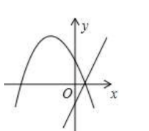 
已知抛物线 $y=3(x-2)^2$ 上的两点 $A\left(x_1, y_1\right), \quad\left(x_2, y_2\right)$, 如果 $x_1 < x_2 < 2$, 那么下列结论 成立的是
$\text{A.}$ $y_1 < y_2 < 0$
$\text{B.}$ $0 < y_1 < y_2$
$\text{C.}$ $0 < y_2 < y_1$
$\text{D.}$ $y_2 < y_1 < 0$
二次函数 $y=-x^2+(k+1) x+1$ 的图象上, 当 $x < 3$ 时, $y$ 随 $x$ 的增大而增大, 则 $k$ 的 取偗范围是
$\text{A.}$ $k=5$
$\text{B.}$ $k \leq 5$
$\text{C.}$ $k=3$
$\text{D.}$ $k \geq 5$
填空题 （共 7 题 ），请把答案直接填写在答题纸上
方程 $(x+1)(x-1)=1$ 转化为一元二次方程的一般形式是
关于 $x$ 的方程 $(a-5) x^2-4 x-1=0$ 有实数根, 则 $a$ 满足
抛物线 $y=c x^2+b x+c$ 经过点 $(2,5),(4,5)$, 则这条抛物线的对称轴是直线
已知抛物线 $y=x^2+m x+n$ 与直线 $y=5$ 的交点坐标为 $(1,5),(-3,5)$, 则方程 $x^2+m x+n-5=0$ 的根是
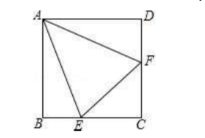
如图, 在正方形 $A B C D$ 中, $E$ 为 $B C$ 上的点, $F$ 为 $C D$ 边上的点, 且 $A E=A F, A B=4$, 设 $E C=x, \triangle A E F$ 的面积为 $y$, 则 $y$ 与 $x$ 之间的函数关系式是
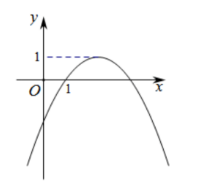
在平面直角坐标系 $x O y$ 中, 二次函数 $y=a x^2+b x+c(a \neq 0)$ 的大致图象如图所示, 则 下列结论正确的是 (填序号).
(1) $a < 0, b < 0, c>0$;
(2) $-\frac{b}{2 a}=1$
(3) $a+b+c < 0$;
(4) $-\frac{b}{2 a}>1$;
(5) $a-b+c < 0$
二次函数 $y=a \times 2+b x+c(a \neq 0)$ 的图象如图所示, 根据图像解答下列问题:
(1)方程 $\mathrm{ax2}+\mathrm{bx}+\mathrm{c}=0$ 的两个根为
(2)不等式 $a \times 2+b x+c>0$ 的解集为
(3)y 随 $\mathrm{x}$ 的增大而减小的自变量 $\mathrm{x}$ 的取值范围为
(4)若方程 $a \times 2+b x+c=k$ 有两个不相等的实数根, 则 $k$ 的取值范围为
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
用适当的方法解方程:
(1) $x^2-4 x+1=0$
(2) $2 x^2-x-15=0$
关于 $x$ 的方程 $x^2+m^2 x-2=0$ 的一个根是 1 , 求方程的另一个根及 $m$ 的值.
已知抛物线与 $x$ 轴相交于 $A(-1,0), B(3,0))$ 两点, 顶点坐标为 $C(1,4)$
(1)求该拋物线解析式:
(2)判断开口方向以及增戙情况:
(3)当 $y < 0$ 时, 直接写出 $x$ 取值范围.
已知拋物线 $y=a x^2+6 x-8$ 与直线 $y=-3 x$ 相交于点 $A(1, m)$.
(1)求拋物线的解析式;
(2)请问(1)中的拋物线经过怎样的平移就可以得到 $y=x^2$ 的图像.
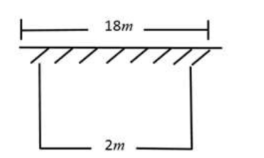
如图, 有一面积是 150 平方米的长方形鸡场, 鸡场的一边靠墙 (墻长 18 米), 垥对 面有一个 2 米宽的门, 另三边用竹篱笆围成, 篱笆总长 33 米, 求: 鸡场的长和宽各为多少米？
已知关于 $x$ 的一元二次方程 $x^2-2 x-3 m^2=0$.
(1)求证: 方程总有两个不相等的实数根;
(2) 若方程的两个实数根分别为 $\alpha, \beta$, 且 $\alpha+2 \beta=5$, 求 $m$ 的值.
某商品的进价为每件 40 元, 售价为每件 50 元, 每个月可卖出 210 件: 如果每件商 品的售价每上涨 1 元, 则每个月少卖 10 件 (每件售价不能高于 65 元). 设每件商品的 售价上涨 $x$ 元 ( $x$ 为正整数). 每件商品的售价定为多少元时, 每个月的利润恰为 2200 元?
已知, 如图, 抛物线 $y=a x^2-2 a x+c(a>0)$ 与 $y$ 轴交于点 $C$, 与 $x$ 轴交于 $A, B$ 两点,
点 $A$ 在点 $B$ 左侧. 点 $\mathrm{A}$ 的坐标为 $(-1,0), O C=3 O A$
(1)求抛物线的解析式:
(2)若点 $D$ 是线段 $B C$ 下方抛物线上的动点, 求四边形 $A B D C$ 面积的最大值:
(3)若抛物线上有一点 $M$, 使 $\angle A C M=45^{\circ}$, 求 $M$ 点坐标.
