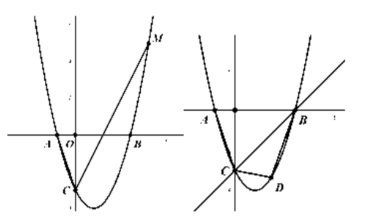
已知, 如图, 抛物线 $y=a x^2-2 a x+c(a>0)$ 与 $y$ 轴交于点 $C$, 与 $x$ 轴交于 $A, B$ 两点,
点 $A$ 在点 $B$ 左侧. 点 $\mathrm{A}$ 的坐标为 $(-1,0), O C=3 O A$
(1)求抛物线的解析式:
(2)若点 $D$ 是线段 $B C$ 下方抛物线上的动点, 求四边形 $A B D C$ 面积的最大值:
(3)若抛物线上有一点 $M$, 使 $\angle A C M=45^{\circ}$, 求 $M$ 点坐标.
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$