单选题 (共 8 题 ),每题只有一个选项正确
下列方程是关于 $x$ 的一元二次方程的是 ( )
$\text{A.}$ $x^2+\frac{1}{x^2}=0$
$\text{B.}$ $\mathrm{a} x^2+\mathrm{b} x+\mathrm{c}=0$
$\text{C.}$ $(x-1)(x+2)=0$
$\text{D.}$ $3 x^2-2 x y-5 y^2=0$
抛物线 $y=x^2+4 x+4$ 与 $x$ 轴的交点情况是 ( )
$\text{A.}$ 没有交点
$\text{B.}$ 有唯一的交点
$\text{C.}$ 有两个不同的交点
$\text{D.}$ 以上结果都有可能
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}$, 将 Rt $\triangle A B C$ 绕点 $C$ 按 顺时针方向旋转一定角度得到 Rt $\triangle D E C$, 点 $D$ 恰好落在边 $A B$ 上. 若 $\angle B=20^{\circ}$, 则 $\angle B C E$ 的度数为

$\text{A.}$ $20^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $80^{\circ}$
将一元二次方程 $x^2-6 x+5=0$ 配方后, 原方程变形为
$\text{A.}$ $(x-6)^2=5$
$\text{B.}$ $(x-3)^2=4$
$\text{C.}$ $(x-6)^2=4$
$\text{D.}$ $(x-3)^2=5$
已知二次函数的图象如图所示, 那么此函数的解析式只 可能是()

$\text{A.}$ $y=-x^2+x+3$
$\text{B.}$ $y=-x^2-3 x-3$
$\text{C.}$ $y=-x^2-x+3$
$\text{D.}$ $y=x^2+x+3$
三角形两边的长是 4 和 9 , 第三边满足方程 $x^2-24 x+140=0$, 则三角形周长为 ( )
$\text{A.}$ 27
$\text{B.}$ 23
$\text{C.}$ 23 或 27
$\text{D.}$ 以上都不对
将抛物线 $y=-2 x^2+3$ 先向右移动 5 个单位长度, 再向上移动 5 个单位长度到的新拋物 线的函数表达式是 ()
$\text{A.}$ $y=-2(x+3)^2-2$
$\text{B.}$ $y=-2(x+3)^2+8$
$\text{C.}$ $\mathrm{y}=-2(x-5)^2-2$
$\text{D.}$ $y=-2(x-5)^2+8$
已知二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图象如图所示, 对称轴为 直线 $x=1$, 与 $x$ 轴的一个交点为 $(3,0)$. 下列结论:
(1) $\mathrm{b}^2-4 \mathrm{ac} < 0$;
(2) $4 \mathrm{a}+2 \mathrm{~b}+\mathrm{c}>0$;
(3)图象与 $x$ 轴的另一个交点为 $(-1,0)$;
(4)当 $x>0$ 时, y 随 $x$ 的增大而 小,
所有正确结论的序号是 ()

$\text{A.}$ (1) (3)
$\text{B.}$ (1) (4)
$\text{C.}$ (2) (3)
$\text{D.}$ (2)(4)
填空题 (共 9 题 ),请把答案直接填写在答题纸上
若函数 $\mathrm{y}=(\mathrm{m}-1) x^{\mathrm{m}^2+1}-x-20$ 是二次函数, 则 $\mathrm{m}$ 的值为
方程 $2(x+1)^2=(x+2)(x-2)$ 化为一般形式为
已知二次函数 $\mathrm{y}$ 与自变量 $x$ 的部分对应值如表:

则此抛物线的顶点坐标为
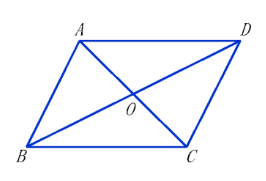
$\triangle A O B$ 与 $\triangle C O D$ 关于公共顶点 $O$ 成中心对称, 连接 $A D 、 B C$, 则四边形 $A B C D$ 是 ( ) 形.
已知函数 $y=-(x-1)^2$ 图象上两点 $A\left(2, y_1\right) B\left(a, y_2\right)$, 其中 $a>2$, 则 $y_1 y_2$ (填 $ > < $ 或 $=)$.
已知二次函数 $\mathrm{y}=x^2-\mathrm{a} x+4$ 的图象与直线 $\mathrm{y}=\mathrm{a} x$ 有且只有 1 个交点, 则 $\mathrm{a}$ 的值为
已知 $\odot O$ 的直径 $A B=10, C D$ 是 $\odot 0$ 的弦, $C D \perp A B$, 垂足为点 $E$, 若 $C D=6$, 则线 段 $\mathrm{AE}$ 的长为
某农机厂四月份生产零件 50 万个, 第二季度共生产零件 182 万个, 设该厂五、六 月份平均每月的增长率 $x$, 依题意列方程, 化为一般形式为
已知二次函数 $y=x^2+4 x-6$.
(1) 将二次函数的解析式化为 $\mathrm{y}=\mathrm{a}(x-\mathrm{h})^2+\mathrm{k}$ 的形式;
(2) 写出二次函数图象的开口方向、对称轴、顶点坐标.
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
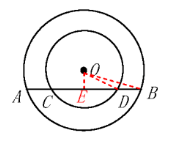
已知在以点 O 为圆心的两个同心圆中, 大圆的弦 $A B$ 交小圆于点 $C, D$ (如图).
(1) 求证: $A C=B D$;
(2) 若大圆的半径 $R=10$, 小圆的半径 $r=8$, 且圆心 0 到直线 $\mathrm{AB}$ 的距离为 6 , 求 $\mathrm{AC}$ 的长.
关于 $x$ 的一元二次方程 $\mathrm{k} x^2+5 x-2=0$ 有两个实数根.
(1) 求实数 $k$ 的取值范围;
(2) 若方程两实根 $x_1 、 x_2$ 满足 $x_1+x_2-x_1^2 x_2^2=1$, 求 $\mathrm{k}$ 的值.
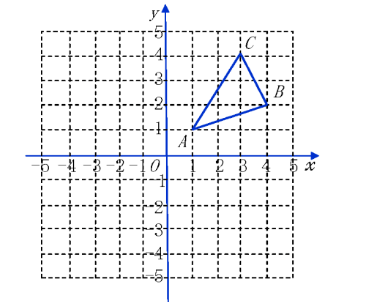
如图, $\triangle \mathrm{ABC}$ 三个顶点的坐标分别为 $\mathrm{A}(1,1), \mathrm{B}(4,2), \mathrm{C}(3,4)$.
(1) 请画出 $\triangle \mathrm{ABC}$ 向左平移 6 个单位长度, 再向下平移 5 个单位长度后得到的 $\triangle \mathrm{A}_{\mathrm{B}} \mathrm{B}_{\mathrm{I}} \mathrm{C}_1$;
(2) 请画出 $\triangle \mathrm{ABC}$ 绕原点逆时针旋转 $90^{\circ}$ 后得到的 $\triangle \mathrm{A}_3 \mathrm{~B}_2 \mathrm{C}_2$;
(3) 在平面内有一动点 $P$, 使得以点 $P 、 A 、 B 、 C$ 为顶点的四边形是平行四边形, 满足 条件的点 $P$ 的个数为 ( ) 个, 它们的坐标分别是 ( )
如图, $\odot 0$ 的直径 $\mathrm{AB}$ 为 10 厘米, 弦 $\mathrm{AC}$ 为 6 厘米, $\angle \mathrm{ACB}$ 的平分线交 $\odot O$ 于 $\mathrm{D}$.
(1) 连接 $\mathrm{AD}, \mathrm{BD}$, 判断 $\triangle \mathrm{ABD}$ 的形状, 并说明理由;
(2) 求弦 CD 的长.

为满足市场需求, 某服装超市在六月初购进一款短袖 $\mathrm{T}$ 恤衫, 每件进价是 80 元, 超市规定每件售价不得少于 90 元, 根据调查发现: 当售价定为 90 元时, 每周 可卖出 600 件, 一件 T 恤衫售价每提高 1 元, 每周要少卖出 10 件.
(1) 试求出每周的销售量 $y$ (件) 与每件售价 $x$ 元之间的函数表达式; (不需要写出自变量 取值范围)
(2) 该服装超市每周想从这款 T 恤衫销售中获利 8250 元, 又想尽量给客户实惠, 该如 何给这款 T 恤衫定价?
(3) 超市管理部门要求这款 $\mathrm{T}$ 恤衫售价不得高于 110 元, 则当每件 $\mathrm{T}$ 恤衫售价定为多少 元,每周的销售利润最大?最大利润是多少?
如图, 已知抛物线 $y=x^2+b x+c$ 的对称轴为直线 $x=-1$. 抛物线与 $x$ 轴相交于 $\mathrm{A}$, $B$ 两点, 点 $A$ 在点 $B$ 的左侧, 点 $C(0,-3)$ 为拋物线与 $y$ 轴的交点.
(1) 求 $\mathrm{b}$ 和 $\mathrm{C}$ 的值;
(2) 在抛物线的对称轴上存在一点 $P$, 使 $P B+P C$ 最短, 请求出点 $P$ 的坐标;
(3) 抛物线上是否存在一点 $Q$, 使 $\triangle Q O A$ 的面积等于 $\triangle B O C$ 的面积的 4 倍? 若存在. 求出 点Q所有的坐标; 若不存在, 请说明理由.
