单选题 (共 8 题 ),每题只有一个选项正确
若集合 $M=\{x \mid \ln x < 1\}, N=\left\{x \mid \frac{x+1}{x} < 2\right\}$, 则 $M \cap N=$
$\text{A.}$ $\{x \mid x>1\}$
$\text{B.}$ $\{x \mid 1 < x < \mathrm{e}\}$
$\text{C.}$ $\{x \mid x < \mathrm{e}\}$
$\text{D.}$ $\Phi$
设 $a>0, b>0$, 则 $a \ln a < b \ln b$ 是 $b>a>1$ 的 ( ) 条件
$\text{A.}$ 充分不必要
$\text{B.}$ 必要不充分
$\text{C.}$ 充要
$\text{D.}$ 既不充分也不必要
在 $\triangle A B C$ 中, $\angle C A B=60^{\circ}, A B=2, A C=1, D$ 为边 $B C$ 上一点, 且 $C D=2 B D$, 则 $|\overrightarrow{A D}|=$
$\text{A.}$ $\frac{\sqrt{21}}{3}$
$\text{B.}$ $\frac{2 \sqrt{3}}{3}$
$\text{C.}$ $\frac{\sqrt{7}}{3}$
$\text{D.}$ $\frac{\sqrt{5}}{3}$
已知 $f(x)=|\lg x|-c$ 有两个下不同零点 $a, b$, 则下列结论成立的是
$\text{A.}$ $a^2+b^2$ 最小值为 2
$\text{B.}$ $a+b$ 最小值为 2
$\text{C.}$ $4 a^2+b^2$ 最小值为 4
$\text{D.}$ $a^2+b^2-a b$ 最小值为 1
已知等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_3=4, S_6=12$, 则 $S_{12}=$
$\text{A.}$ 32
$\text{B.}$ 28
$\text{C.}$ 48
$\text{D.}$ 60
已知 $a=\mathrm{e}^{-\frac{2021}{202}}, b=\frac{1}{2022}, c=\ln \frac{2023}{2022}$, 则 $a, b, c$ 的大小关系为
$\text{A.}$ $a>b>c$
$\text{B.}$ $a>c>b$
$\text{C.}$ $c>a>b$
$\text{D.}$ $b>c>a$
已知函数 $f(x)=\sin (\omega x+\theta),\left(\omega>0,|\theta| < \frac{\pi}{2}\right), x=\frac{\pi}{6}$ 是 $f(x)$ 的一个极值点, $x=-\frac{\pi}{6}$ 是与其相邻的一个零点, 则 $f\left(\frac{\pi}{3}\right)$ 的值为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ $-1$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
已知数列 $\left\{a_n\right\}$ 满足 $a_n \cdot(-1)^n+a_{n+2}=2 n-1, S_{20}=650$, 则 $a_{23}=$
$\text{A.}$ 231
$\text{B.}$ 234
$\text{C.}$ 279
$\text{D.}$ 276
多选题 (共 4 题 ),每题有多个选项正确
下列区间中能使函数 $y=\lg \left(x^3-x^2-x+1\right)$ 单调递增的是
$\text{A.}$ $[-1,+\infty)$
$\text{B.}$ $(2,+\infty)$
$\text{C.}$ $\left(-2,-\frac{1}{3}\right)$
$\text{D.}$ $\left(-1,-\frac{1}{2}\right)$
下列各式中, 值为 $\sqrt{3}$ 的是
$\text{A.}$ $2\left(\cos ^2 \frac{\pi}{12}-\cos ^2 \frac{5 \pi}{12}\right)$
$\text{B.}$ $\frac{1+\tan 15^{\circ}}{1-\tan 15^{\circ}}$
$\text{C.}$ $\cos 15^{\circ}-\sqrt{3} \sin 15^{\circ}$
$\text{D.}$ $16 \sin 10^{\circ} \cos 20^{\circ} \cos 30^{\circ} \cos 40^{\circ}$
在平面四边形 $A B C D$ 中, $\overrightarrow{A B} \cdot \overrightarrow{B C}=0, \overrightarrow{A D} \cdot \overrightarrow{C D}=0,|\overrightarrow{A B}|=|\overrightarrow{A D}|=1, \overrightarrow{A D} \cdot \overrightarrow{B A}=\frac{1}{2}$, 若 点 $E$ 为线段 $C D$ 上的动点, 则 $\overrightarrow{A E} \cdot \overrightarrow{B E}$ 的值可能为
$\text{A.}$ 1
$\text{B.}$ $\frac{21}{16}$
$\text{C.}$ 2
$\text{D.}$ $\frac{7}{2}$
已知函数 $y=f(x)$ 对于任意的 $x \in\left(0, \frac{\pi}{2}\right)$, 均满足 $f^{\prime}(x) \cos x+f(x) \sin x=\ln x$, 其中 $f^{\prime}(x)$ 是 $f(x)$ 的导函数, 则下列不等式成立的是
$\text{A.}$ $\sqrt{2} f\left(\frac{\pi}{6}\right)>\sqrt{3} f\left(\frac{\pi}{4}\right)$
$\text{B.}$ $2 f\left(\frac{\pi}{12}\right)>(\sqrt{3}+1) f\left(\frac{\pi}{4}\right)$
$\text{C.}$ $(\sqrt{3}-1) f\left(\frac{\pi}{3}\right) < \sqrt{2} f\left(\frac{5 \pi}{12}\right)$
$\text{D.}$ $(\sqrt{3}-1) f\left(\frac{\pi}{3}\right)>\sqrt{2} f\left(\frac{5 \pi}{12}\right)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $a, b$ 且 $|a|=1,|b|=2, a, b$ 的夹角为 $60^{\circ}$, 则 $|2 a+b|$
等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 公差 $d>0 . a_1, a_4$ 是函数 $f(x)=4 \ln x+\frac{1}{2} x^2-5 x$ 的极值 点, 则 $S_6=$
已知函数 $f(x)=\mathrm{e}^x-\mathrm{e}^{-x}-2 x+1$, 则不等式 $f(2 x-3)+f(x)>2$ 的解集为
对任意的 $x>1$, 不等式 $\frac{1}{a} \mathrm{e}^x-\ln (x-1)-5+2 \ln a \geqslant 0$ 恒成立, 则 $a$ 的范围为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为 $a, b, c$. 已知向量 $m=(b, a)$, $\boldsymbol{n}=(\sin A, \sqrt{3} \cos (A+C))$ 且 $\boldsymbol{m} \cdot \boldsymbol{n}=0$
(1) 求角 $B$ 的大小;
(2) 若 $b=\sqrt{3}$, 求 $3 a+c$ 的最大值.
已知数列 $\left\{a_n\right\}$ 各项均为正数且满足 $a_n^2-(n-1) a_n-2 n^2+n=0$, 数列 $\left\{b_n\right\}$ 满足 $b_1=3$, 且 $b_{n+1}=3 b_n+3^{n+1}$.
(1) 求 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2) 若 $c_n=b_n+a_n$, 求 $\left\{c_n\right\}$ 的前 $n$ 项和 $T_n$.
已知函数 $f(x)=\left(x^2-a x\right) \ln x-\frac{3}{2} x^2+2 a x$
(1)记 $f^{\prime}(x)=g(x)$, 若对定义域内任意的 $x, g(x) \geqslant 0$ 恒成立,求实数 $a$ 的范围;
(2)试讨论函数 $f(x)$ 的单调性.
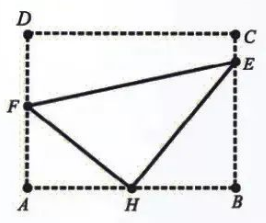
如图, 我市某污水处理厂要在一个矩形污水处理池 $A B C D$ 的池底水平铺设 污水净化管道(Rt $\triangle F H E$ 三条边, $H$ 是直角顶点) 来处理污水, 管道越长, 污水净化效果越 好. 要求管道的接口 $H$ 是 $A B$ 的中点, 点 $E, F$ 分别落在线段 $B C, A D$ 上, 已知 $A B=20 \mathrm{~m}$, $A D=10 \sqrt{3} \mathrm{~m}$, 记 $\angle B H E=\theta$.
(1) 试将污水净化管道的总长度 $L$ (即 Rt $\triangle F H E$ 的周长) 表示为 $\theta$ 的函数,并求出定义域;
(2) 问 $\theta$ 取何值时, 污水净化效果最好? 并求出此时管道 的总长度.
已知函数 $f(x)=\mathrm{e}^x(\sin x+\cos x)-2 x$
(1) 求 $f(x)$ 在 $(0, f(0))$ 处的切线方程;
(2) 求 $f(x)$ 在 $\left[0, \frac{\pi}{2}\right]$ 上的最小值 (参考数据: $\mathrm{e}=2.71828 \cdots$ )
已知数列 $\left\{a_n\right\}, a_1=1, S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 且 $S_n=\frac{1}{3}(n+2) a_n$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 求证: $\sin a_n-a_n < 0$;
(3) 证明: $\left(1+\sin \frac{1}{a_1}\right)\left(1+\sin \frac{1}{a_2}\right)\left(1+\sin \frac{1}{a_3}\right) \cdots\left(1+\sin \frac{1}{a_n}\right) < \mathrm{e}^2$.