单选题 (共 8 题 ),每题只有一个选项正确
设集合 $M=\{-2,4,7\}, N=\left\{x \mid x^2-3 x-n=0\right\}$, 若 $M \cap N=\{4\}$, 则 $N=$
$\text{A.}$ $\{-3,4\}$
$\text{B.}$ $\{2,4\}$
$\text{C.}$ $\{1,4\}$
$\text{D.}$ $\{-1,4\}$
命题 " $\exists x \in[-1,2], \frac{1}{2} x^2-a \leqslant 0$ " 是真命题的一个充分不必要条件是
$\text{A.}$ $a \geqslant 0$
$\text{B.}$ $a \geqslant-3$
$\text{C.}$ $a \leqslant 0$
$\text{D.}$ $a \geqslant 3$
已知奇函数 $f(x)=\left(2^x+m \cdot 2^{-x}\right) \cos x$, 则 $m=$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ $\frac{1}{2}$
若函数 $h(x)=\ln x-2 a x$ 在 $[1,3]$ 上不单调, 则实数 $a$ 的取值范围为
$\text{A.}$ $\left(\frac{1}{6}, \frac{1}{2}\right)$
$\text{B.}$ $\left[\frac{1}{6}, \frac{1}{2}\right]$
$\text{C.}$ $(-\infty, 1)$
$\text{D.}$ $\left(\frac{1}{6},+\infty\right)$
已知 $\sin \alpha+\sqrt{3} \cos \alpha=\frac{2}{3}$, 则 $\cos \left(4 \alpha+\frac{\pi}{3}\right)=$
$\text{A.}$ $-\frac{63}{65}$
$\text{B.}$ $-\frac{17}{81}$
$\text{C.}$ $\frac{24}{25}$
$\text{D.}$ $\frac{4}{5}$
设 $S_n$ 是数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 且 $a_1=1, S_n=\left(2 S_n+1\right) S_{n+1}$, 则 $\frac{a_5}{S_{11}}=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $-\frac{2}{3}$
$\text{C.}$ $-2$
$\text{D.}$ $-\frac{3}{4}$
已知函数 $f(x)= e ^{2 x}-2 a e ^x-4 a^2 x(a>0)$, 若函数 $f(x)$ 的值域与 $f(f(x))$ 的值域相同, 则 $a$ 的取值范围是
$\text{A.}$ $\left(0, \frac{1}{2}\right)$
$\text{B.}$ $(0,1]$
$\text{C.}$ $\left[\frac{1}{2},+\infty\right)$
$\text{D.}$ $(1,+\infty)$
已知 $\omega>0$, 函数 $f(x)=\sin \omega x$ 与 $g(x)=\cos \omega x$ 的图像在 $[\pi, 2 \pi]$ 上最多有两个公共点, 则 $\omega$的取值范围为
$\text{A.}$ $\left(0, \frac{17}{8}\right) \cup\left(\frac{9}{4}, \frac{21}{8}\right)$
$\text{B.}$ $\left(0, \frac{5}{4}\right] \cup\left(\frac{9}{4}, \frac{17}{8}\right]$
$\text{C.}$ $\left(0, \frac{1}{4}\right] \cup\left(\frac{5}{4}, \frac{17}{8}\right)$
$\text{D.}$ $\left(0, \frac{17}{8}\right] \cup\left(\frac{9}{4}, \frac{5}{2}\right)$
多选题 (共 3 题 ),每题有多个选项正确
若 $a, b \in R$, 则下列命题正确的是
$\text{A.}$ 若 $a b \neq 0$ 且 $a < b$, 则 $\frac{1}{a}>\frac{1}{b}$
$\text{B.}$ 若 $a < b$, 则 $a^3 < b^3$
$\text{C.}$ 若 $a|a| < b|b|$, 则 $a < b$
$\text{D.}$ 若 $a>b>0$, 则 $\frac{b+1}{a+1} < \frac{b}{a}$
已知函数 $\varphi(x)$ 的定义域为 $R$, 对于 $\forall x, y \in R$, 恒有 $\varphi(x+y)=\varphi(x)+\varphi(y)-t$, 且当 $x>0$时, $\varphi(x) < t$, 则下列命题正确的有
$\text{A.}$ $\varphi(0) = t$
$\text{B.}$ $\varphi(x)=\varphi(2 t-x)$
$\text{C.}$ $\varphi(-2024)=2 t-\varphi(2024)$
$\text{D.}$ $\forall x \neq y \in R ,(x-y)[\varphi(x)-\varphi(y)] < 0$
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n,(3 n+2) S_{n+1}+(3 n-1) S_{n-1}=(6 n+1) S_n(n \in N$, 且 $n \geqslant 2)$,若 $a_1=\frac{1}{2}, a_2=\frac{1}{5}$, 则下列说法正确的是
$\text{A.}$ $a_5=\frac{1}{14}$
$\text{B.}$ 数列 $\left\{\frac{1}{a_n}\right\}$ 为等差数列
$\text{C.}$ 数列 $\left\{\frac{a_n}{a_{n+1}^2}\right\}$ 中的最小项为 12
$\text{D.}$ 数列 $\left\{\frac{(-1)^n}{a_n a_{n+1}}\right\}$ 的前 $2 n$ 项和 $T_{2 n}$ 为 $18 n^2+12 n$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
函数 $y=\log _{2024}\left(a x^2+x+1\right)$ 的值域为 $R$, 则实数 $a$ 的取值范围是
已知 $a_1=1, a_2=2$, 且 $a_{n+1}=a_n+a_{n+2}$ ( $n$ 为正整数), 则 $a_{2029}=$
已知不等式 $\frac{a+2 \ln x-2}{x^2} \leqslant e ^x-\frac{1}{x}$ 恒成立, 则实数 $a$ 的取值范围为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\sin \left(\omega x+\frac{\pi}{6}\right)-\sin \left(\omega x-\frac{\pi}{3}\right)(\omega>0)$.
(1) 当 $\omega=2$ 时,求 $f(x)$ 的对称轴方程和最大值;
(2) 若 $\omega \in N ^{\cdot}$, 且 $f(x)$ 在区间 $\left(-\frac{\pi}{2}, 0\right)$ 上单调递增, 求 $f(x)$ 在区间 $\left(0, \frac{4 \pi}{3}\right)$ 上的极值点个数。
已知函数 $f(x)=\log _2\left[4^x+(a+2) \cdot 2^x+a+1\right]$.
(1) 若 $a=0$, 求满足 $2 < f(x) < 4$ 的 $x$ 的取值范围;
(2)若对任意 $x \geqslant 1, f(x) \geqslant x$ 恒成立, 求 $a$ 的取值范围.
已知函数 $f(x)=\cos x+a x-1$.
(1) 当 $a=1$ 时, 求曲线 $y=f(x)$ 在点 $(\pi, f(\pi))$ 处的切线方程;
(2) 当 $a=\frac{1}{2}$ 时, 求 $f(x)$ 在区间 $(0,+\infty)$ 上的零点个数.
设 $S_n, T_n$ 分别为数列 $\left\{a_n\right\},\left\{b_n\right\}$ 的前 $n$ 项和, $2 a_{n+1}-a_n=\frac{1}{2^{n+1}}, a_1=\frac{3}{4}$, 数列 $\left\{b_n\right\}$ 是公比为 $-\frac{2}{3}$ 的等比数列, $8 S_2=9 T_2$.
(1) 求 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2) 比较 $S_n$ 和 $T_n$ 的大小.
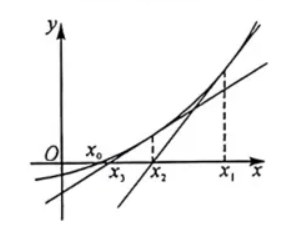
如图, 在求解一些函数零点的近似值时, 常用牛顿切线法进行求解. 牛顿切线法的计算过程如下: 设函数 $f(x)$ 的一个零点 $x_0$, 先取定一个初值 $x_1$, 曲线 $y=f(x)$ 在 $x=x_1$ 处的切线为 $l_1$, 记 $l_1$ 与 $x$ 轴的交点横坐标为 $x_2$, 曲线 $y=f(x)$ 在 $x=x_2$ 处的切线为 $l_2$, 记 $l_2$ 与 $x$ 轴的交点横坐标为 $x_3$, 以此类推, 每进行一次切线求解, 我们就称之为进行了一次迭代, 若进行足够多的迭代次数, 就可以得到 $x_0$ 的近似值 $x_n\left(n \in N ^*\right)$, 设函数 $f(x)=x^3+x-1$, 令 $x_1=1$.
(1) 证明: $f(x)$ 存在唯一零点 $x_0$, 且 $\frac{2}{3} < x_0 < 1$;
(2) 已知 $x_n>\frac{2}{3}$, 证明: $\left|x_{n+1}-x_0\right| < \left|x_n-x_0\right|^2$;
(3) 经过 4 次迭代后,判断 $x_0$ 的近似值 $x_5$ 与 $x_0$ 的差值小于 $10^{-1}$.