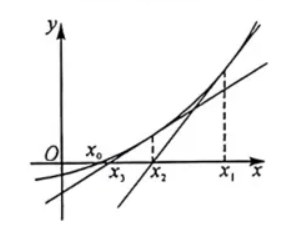
如图, 在求解一些函数零点的近似值时, 常用牛顿切线法进行求解. 牛顿切线法的计算过程如下: 设函数 $f(x)$ 的一个零点 $x_0$, 先取定一个初值 $x_1$, 曲线 $y=f(x)$ 在 $x=x_1$ 处的切线为 $l_1$, 记 $l_1$ 与 $x$ 轴的交点横坐标为 $x_2$, 曲线 $y=f(x)$ 在 $x=x_2$ 处的切线为 $l_2$, 记 $l_2$ 与 $x$ 轴的交点横坐标为 $x_3$, 以此类推, 每进行一次切线求解, 我们就称之为进行了一次迭代, 若进行足够多的迭代次数, 就可以得到 $x_0$ 的近似值 $x_n\left(n \in N ^*\right)$, 设函数 $f(x)=x^3+x-1$, 令 $x_1=1$.
(1) 证明: $f(x)$ 存在唯一零点 $x_0$, 且 $\frac{2}{3} < x_0 < 1$;
(2) 已知 $x_n>\frac{2}{3}$, 证明: $\left|x_{n+1}-x_0\right| < \left|x_n-x_0\right|^2$;
(3) 经过 4 次迭代后,判断 $x_0$ 的近似值 $x_5$ 与 $x_0$ 的差值小于 $10^{-1}$.
(1) 证明: $f(x)$ 存在唯一零点 $x_0$, 且 $\frac{2}{3} < x_0 < 1$;
(2) 已知 $x_n>\frac{2}{3}$, 证明: $\left|x_{n+1}-x_0\right| < \left|x_n-x_0\right|^2$;
(3) 经过 4 次迭代后,判断 $x_0$ 的近似值 $x_5$ 与 $x_0$ 的差值小于 $10^{-1}$.
