单选题 （共 17 题 ），每题只有一个选项正确
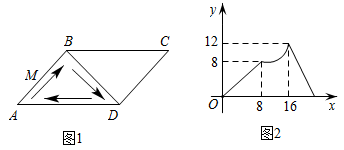
如图 1, 四边形 $A B C D$ 是平行四边形, 连接 $B D$, 动点 $M$ 从点 $A$ 出发沿折线 $A B \rightarrow B D \rightarrow D A$匀速运动, 回到点 $A$ 后停止. 设点 $M$ 运动的路程为 $x$, 线段 $A M$ 的长为 $y$, 图 2 是 $y$ 与 $x$ 的函数关系的大致图像, 则 $Y A B C D$ 的面积为
$\text{A.}$ $24 \sqrt{7}$
$\text{B.}$ $16 \sqrt{7}$
$\text{C.}$ $12 \sqrt{7}$
$\text{D.}$ 36
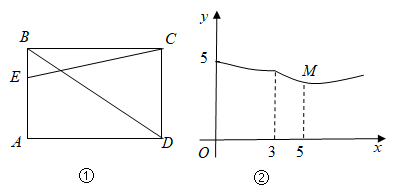
如图 ① , 矩形 $A B C D$ 中, 点 $E$ 沿折线 $A-B-D$ 从点 $A$ 匀速运动到点 $D$, 连接 $C E$, 设点 $E$运动的路程为 $x$, 线段 $C E$ 的长度为 $y$, 图 ② 是点 $E$ 运动时 $y$ 随 $x$ 变化的关系图象, 当 $x=3$时, 点 $E$ 与点 $B$ 重合, 则点 $M$ 的纵坐标为
$\text{A.}$ $\frac{6 \sqrt{3}}{5}$
$\text{B.}$ $\frac{5}{2}$
$\text{C.}$ $\frac{6 \sqrt{5}}{5}$
$\text{D.}$ 3
已知: $Rt \triangle ABC$ 中, $\angle A C B=90^{\circ}, A C=B C=8 cm, O$ 是 $A B$ 中点, 点 $E 、 F$ 分别从 $B 、 C$两点同时出发, 以 $1 cm / s$ 的速度沿 $B C 、 C A$ 运动, 到点 $C 、 A$ 时停止运动, 设运动时间为 $t(s)$ , $ \triangle OEF$ 的面积为 $S\left(cm^2\right)$, 则能表示 $S$ 与 $t$ 函数关系的图象大致是
$\text{A.}$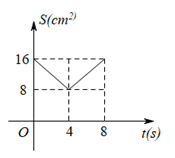 
$\text{B.}$ 
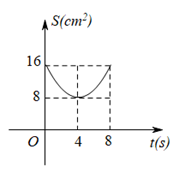$\text{C.}$ 
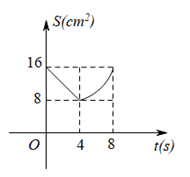$\text{D.}$ 
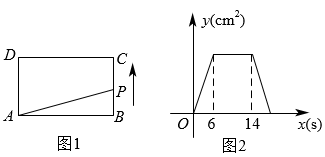
如图 1, 在长方形 $A B C D$ 中, 动点 $P$ 从点 $B$ 出发, 沿 $B \rightarrow C \rightarrow D \rightarrow A$ 方向匀速运动至点 $A$ 停止. 已知点 $P$ 的运动速度为 $1 cm / s$, 设点 $P$ 的运动时间为 $x(s), \triangle P A B$ 的面积为 $y\left(cm^2\right)$,若 $y$ 关于 $x$ 的函数图象如图 2 所示, 则长方形 $A B C D$ 面积为
$\text{A.}$ 20
$\text{B.}$ 28
$\text{C.}$ 48
$\text{D.}$ 24
如图, 正方形 $A B C D$ 中, $A B=8 cm$, 对角线 $A C, B D$ 相交于点 $O$, 点 $E, F$ 分别从 $B, C$ 两点同时出发, 以 $1 cm / s$ 的速度沿 $B C, C D$ 运动, 到点 $C, D$ 时停止运动, 设运动时间为 $t(s), \triangle O E F$的面积为 $S\left( { cm }{ }^2\right)$, 则 $S\left(cm^2\right)$ 与 $t(s)$ 的函数关系可用图像表示为
$\text{A.}$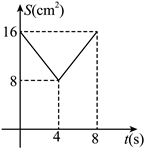 
$\text{B.}$ 
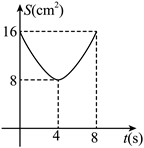$\text{C.}$ 
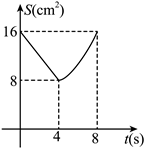$\text{D.}$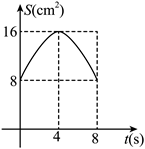 
如图 1, 在 $\triangle A B C$ 中, $A B=B C, B D \perp A C$ 于点 $D(A D>B D)$. 动点 $M$ 从 $A$ 点出发, 沿折线 $A B \rightarrow B C$方向运动, 运动到点 $C$ 停止. 设点 $M$ 的运动路程为 $x, \triangle A M D$ 的面积为 $y, y$ 与 $x$ 的函数图象如图 2, 则 $A D+B D$ 的值为
如图 1, 在 $\triangle A B C$ 中, $A B=B C, B D \perp A C$ 于点 $D(A D>B D)$. 动点 $M$ 从 $A$ 点出发, 沿折线 $A B \rightarrow B C$方向运动, 运动到点 $C$ 停止. 设点 $M$ 的运动路程为 $x, \triangle A M D$ 的面积为 $y, y$ 与 $x$ 的函数图象如图 2, 则 $A D+B D$ 的值为 1
$\text{A.}$ 3
$\text{B.}$ 5
$\text{C.}$ 7
$\text{D.}$ 9
如图 1, 点 F 从菱形 ABCD 的顶点 A 出发, 沿 $A \rightarrow D \rightarrow B$ 以 $1 cm / s$ 的速度匀速运动到点 B ,图2 是点 $F$ 运动时, $\triangle F B C$ 的面积 $y\left(cm^2\right)$ 随时间 $x(s)$ 变化的关系图象, 则 a 的值为
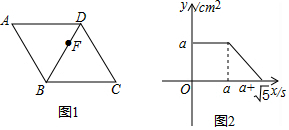
$\text{A.}$ $\sqrt{5}$
$\text{B.}$ 2
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ $2 \sqrt{5}$
如图 ① , 四边形 $A B C D$ 中, $B C \| A D, \angle A=90^{\circ}$, 点 $P$ 从 $A$ 点出发, 沿折线 $A B \rightarrow B C \rightarrow C D$ 运动, 到点 $D$ 时停止, 已知 $\triangle P A D$ 的面积 $s$ 与点 $P$ 运动的路程 $x$ 的函数图象如图(2)所示, 则点 $P$ 从开始到停止运动的总路程为
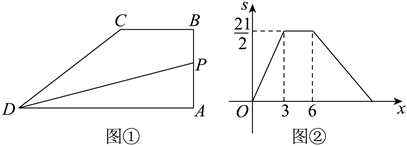
$\text{A.}$ 6
$\text{B.}$ 9
$\text{C.}$ 10
$\text{D.}$ 11
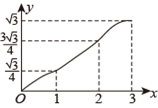
如图 1. 在矩形 $A B C D$ 中, 点 $P$ 从点 $A$ 出发, 匀速沿 $A B \rightarrow B D$ 向点 $D$ 运动, 连接 $D P$, 设点 $P$ 的运动距离为 $x, D P$ 的长为 $y, y$ 关于 $x$ 的函数图象如图 2 所示, 则当点 $P$ 为 $A B$ 中点时, $D P$ 的长为
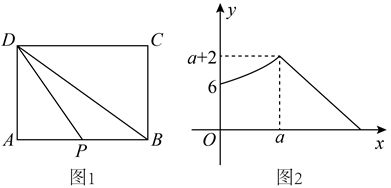
$\text{A.}$ 5
$\text{B.}$ 8
$\text{C.}$ $5 \sqrt{2}$
$\text{D.}$ $2 \sqrt{13}$
如图, 点 $E 、 F$ 分别从矩形的顶点 $B 、 C$ 同时出发, 分别沿 $B C 、 C D$ 以相同的速度向端点 $C$ 、 $D$ 运动, 到达端点后停止, 若线段 $B E$ 的长为 $x, \triangle A E F$ 的面积为 $y$, 且 $y$ 与 $x$ 的函数图像如图所示, 则矩形的周长为
$\text{A.}$ 22
$\text{B.}$ 24
$\text{C.}$ 26
$\text{D.}$ 28
如图(1), 在正方形 $A B C D$ 中, 点 $M$ 是 $A B$ 的中点, 点 $N$ 是对角线 $B D$ 上一动点, 设 $D N=x$, $A N+M N=y$, 已知 $y$ 与 $x$ 之间的函数图象如图(2)所示, 点 $E(a, 2 \sqrt{5})$ 是图象的最低点, 那么 $a$ 的值为
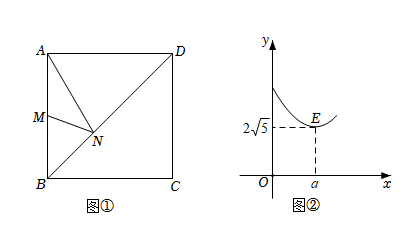
$\text{A.}$ $\frac{8 \sqrt{2}}{3}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ $\frac{4}{3} \sqrt{2}$
$\text{D.}$ $\frac{4}{3} \sqrt{5}$
如图 (1) 所示, $E$ 为矩形 $A B C D$ 的边 $A D$ 上一点, 动点 $P, Q$ 同时从点 $B$ 出发, 点 $P$ 沿折线 $B E-E D-D C$ 运动到点 $C$ 时停止, 点 $Q$ 沿 $B C$ 运动到点 $C$ 时停止, 它们运动的速度都是 $1 cm /$秒, 设 $P 、 Q$ 同时出发 $t$ 秒时, $\triangle B P Q$ 的面积为 $y cm^2$. 已知 $y$ 与 $t$ 的函数关系图象如图 (2) (曲线 $O M$ 为抛物线的一部分) 则下列结论错误的是
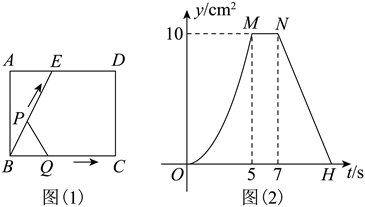
$\text{A.}$ $A B=4 cm$
$\text{B.}$ 当 $5 < t < 7$ 时, $\triangle B P Q$ 的面积是定值
$\text{C.}$ 当 $0 < t \leq 5$ 时, $y=\frac{4}{5} t^2$
$\text{D.}$ 当 $t=\frac{29}{4}$ 秒时, $\frac{B Q}{P Q}=\frac{4}{3}$
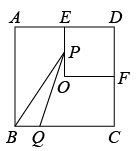
如图, 四边形 $A B C D$ 是边长为 2 cm 的正方形, 点 $E$, 点 $F$ 分别为边 $A D, C D$ 中点, 点 $O$ 为正方形的中心, 连接 $O E, O F$, 点 $P$ 从点 $E$ 出发沿 $E-O-F$ 运动, 同时点 $Q$ 从点 $B$ 出发沿 $B C$ 运动, 两点运动速度均为 $1 cm / s$, 当点 $P$ 运动到点 $F$ 时, 两点同时停止运动, 设运动时间为 $t s$,连接 $B P, P Q, \triangle B P Q$ 的面积为 $S_{ cm }{ }^2$, 下列图像能正确反映出 $S$ 与 $t$ 的函数关系的是
$\text{A.}$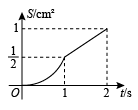 
$\text{B.}$ 
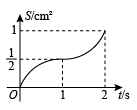$\text{C.}$ 
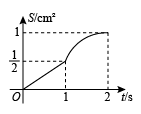$\text{D.}$ 
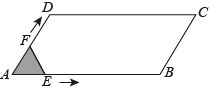
如图, 在 $\square A B C D$ 中, $\angle A=60^{\circ}, A B=2, A D=1$, 点 $E, F$ 在 $\triangle A B C D$ 的边上, 从点 $A$ 同时出发,分别沿 $A \rightarrow B \rightarrow C$ 和 $A \rightarrow D \rightarrow C$ 的方向以每秒 1 个单位长度的速度运动, 到达点 $C$ 时停止, 线段 $E F$ 扫过区域的面积记为 $y$, 运动时间记为 $x$, 能大致反映 $y$ 与 $x$ 之间函数关系的图象是
$\text{A.}$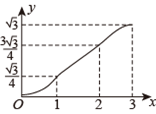 
$\text{B.}$ 
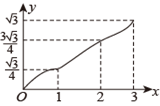$\text{C.}$ 
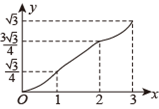$\text{D.}$ 